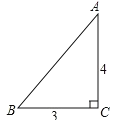
【题目】如图,一张三角形纸片ABC,其中![]() ,
,![]() ,
,![]() 现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处
现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处![]() 这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是
这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
(1)图1,根据折叠得:DE是线段AC的垂直平分线,由中位线定理的推论可知:DE是△ABC的中位线,得出DE的长,即a的长;
(2)图2,同理可得:MN是△ABC的中位线,得出MN的长,即b的长;
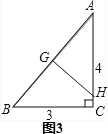
(3)图3,根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即c的长.

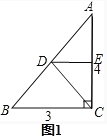 第一次折叠如图1,折痕为DE,
第一次折叠如图1,折痕为DE,
由折叠得:AE=EC=![]() AC=
AC=![]() ×4=2,DE⊥AC ,
×4=2,DE⊥AC ,
∵∠ACB=90°,
∴DE∥BC,
∴a=DE=![]() BC=
BC=![]() ×3=
×3=![]() ,
,
第二次折叠如图2,折痕为MN,
由折叠得:BN=NC=![]() BC=
BC=![]() ×3=
×3=![]() ,MN⊥BC.
,MN⊥BC.
∵∠ACB=90°,
∴MN∥AC,
∴b=MN=![]() AC=
AC=![]() ×4=2,
×4=2,
第三次折叠如图3,折痕为GH,
由勾股定理得:AB=![]() =5,
=5,
由折叠得:AG=BG=![]() AB=
AB=![]() ×5=
×5=![]() ,GH⊥AB,
,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠ACB,
∴△ACB∽△AGH,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴GH=![]() ,即c=
,即c=![]() ,
,
∵2>![]() ,>
,>![]() ,
,
∴b>c>a.
故答案为:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
-
科目: 来源: 题型:
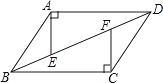
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张直角三角形纸片ABC,边
 ,
, ,
,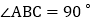 ,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为
,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为


A. 16 B. 17 C. 18 D. 19
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2
 ,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
,∠BAC=120°,点D、E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为_____.
相关试题

