搜索
【题目】已知AB=10cm，点C在直线AB上，如果BC=4cm，点D是线段AC的中点，求线段BD的长度．
参考答案：
【答案】7cm或3cm
【解析】
根据C点在直线AB上的位置分类讨论①当C点在线段AB间时，先算出AC的长，再根据D为AC中点，计算出CD的长，最后计算BC+CD即可；②当C在线段AB外时，先计算AC的长，再根据中点算出CD的长，最后计算CD-BC即可.
（1）当C在线段AB间时
∵AB=10,边长、BC=4cm
∴AC=6cm
又∵点D是AC的中点，
所以AD=CD=
AC=3cm,
∵D是AC的中点，
∴CD=AC=3cm
BD=BC+CD=4+3=7cm
（2）当C在线段AB外时，
∵BC=4，AB=10
∴AC=14
∵D时AC的中点，
CD=AC=7cm
BD=CD-BC=7-4=3cm
故答案是:7cm或3cm
-
科目： 来源： 题型：
查看答案和解析>>【题目】某县对即将参加中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频数分布表和频数分布直方图的一部分．
请根据图表信息回答下列问题：
（1）样本容量为 ；
（2）在频数分布表中，a= ，b= ，并将频数分布直方图补充完整；
（3）若视力在 4.6 以上（含 4.6）均属正常，根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线
与两轴分别交于A、B、C三点，已知点A（一3，O），B(1，0)．点P在第二象限内的抛物线上运动，作PD上
轴子点D，交直线AC于点E．
(1)
(2)过点P作PF⊥AC于点F．求当△PEF的周长取最大值时点P的坐标．
(3)连接AP，并以AP为边作等腰直角△APQ，当顶点Q恰好落在抛物线的对称轴上时，求对应的P点坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A的坐标为（﹣4，4），点B的坐标为（0，2）．
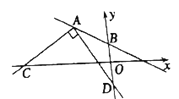
（1）求直线AB的解析式；
（2）如图，以点A为直角顶点作∠CAD＝90°，射线AC交x轴于点C，射线AD交y轴于点D．当∠CAD绕着点A旋转，且点C在x轴的负半轴上，点D在y轴的负半轴上时，OC﹣OD的值是否发生变化？若不变，求出它的值；若变化，求出它的变化范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，连结CD，将线段CD绕点C顺时针旋转90°至CE位置，连接AE．
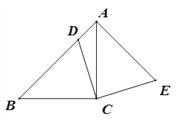
（1）求证：AB⊥AE；
（2）若
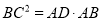，求证：四边形ADCE为正方形． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC内接于⊙O，CD平分∠ACB交⊙O于D，过点D作PQ∥AB分别交CA、CB延长线于P、Q，连接BD．
（1）求证：PQ是⊙O的切线；
（2）求证：BD2=ACBQ；
（3）若AC、BQ的长是关于x的方程
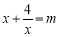的两实根，且tan∠PCD=
，求⊙O的半径．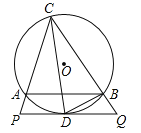
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．
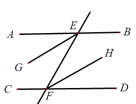
请完成以下证明过程：
证明：∵AB∥CD(已知)
∴∠AEF=∠EFD（__________________）
∵EG平分∠AEF，FH平分∠EFD（__________）
∴∠___＝
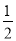∠AEF,∠___= 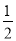∠EFD（____________）∴∠_____=∠______(等量代换)
∴EG∥FH（__________________）．
相关试题
