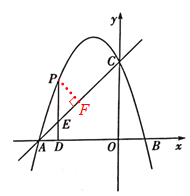
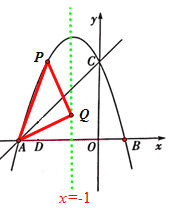
【题目】如图,抛物线![]() 与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上
与两轴分别交于A、B、C三点,已知点A(一3,O),B(1,0).点P在第二象限内的抛物线上运动,作PD上![]() 轴子点D,交直线AC于点E.
轴子点D,交直线AC于点E.

(1) ![]()
(2)过点P作PF⊥AC于点F.求当△PEF的周长取最大值时点P的坐标.
(3)连接AP,并以AP为边作等腰直角△APQ,当顶点Q恰好落在抛物线的对称轴上时,求对应的P点坐标.
参考答案:
【答案】(1) -2; 3 ;(2)( ![]() ,
, ![]() )(3)
)(3) 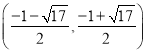 ,
, ![]()
【解析】试题分析:(1)将A、B两点坐标代入解析式中即可求出b、c的值;
(2)通过点P、E的坐标可求出PE=![]() ,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
,由题可知,△PEF为等腰直角三角形,当PE最大时,此三角形的周长最大,求出令PE最大的x值,即可求出P点的坐标;
(3)对以P、Q、A三个顶点的角分别为直角时所形成的等腰直角三角形进行分类讨论即可.
解:(1)∵A(一3,O),B(1,0)在抛物线![]() 的图象上,
的图象上,
∴![]()
解得![]()
故答案为:-2,3 ;
(2)∵C(0,3),A(-3,0)
∴AO=CO
∴∠CAO=45°
∵PD上![]() 轴于点D
轴于点D
∴∠ADE=90°
∴∠AED=45°
∵PF⊥AC于点F
且∠PEF=∠AED=45°
∴△PEF为等腰直角三角形
∴当PE最大时,此三角形的周长最大,
由C(0,3),A(-3,0)可知直线AC的解析式为
![]()
设P(x, ![]() ),则E点坐标为(x,x+3)
),则E点坐标为(x,x+3)
∴PE=![]() (-3<x<0)
(-3<x<0)
∵当![]() 时,PE最大,即此时△PEF的周长取最大值
时,PE最大,即此时△PEF的周长取最大值
∴P点坐标为(![]() ,
,![]() )
)
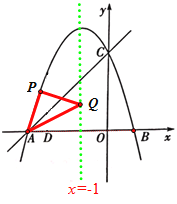
(3)有三种情况:
①当∠APQ=90°且PA=PQ时,P点坐标为
②当∠PAQ=90°且AP=AQ时,P点坐标为![]()
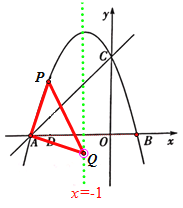
③当∠AQP=90°且PQ=AQ时,P点坐标为![]()
故P点坐标为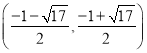 ,
, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.
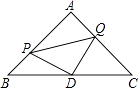
(1)求证:△PDQ是等腰直角三角形;
(2)当点P运动到什么位置时,四边形APDQ是正方形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对60个数据进行处理时,适当分组,各组数据个数之和与百分率之和分别等于( )
A.60,1
B.60,60
C.1,60
D.1,1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)求证:BD是⊙O的切线;
(2)求证:CE2=EHEA;
(3)若⊙O的直径为5,sinA=
 ,求BH的长.
,求BH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成三角形的是( )
A. 1,2,3 B. 3,8,4 C. 6,4,5 D. 5,2,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】医学研究发现一种新病毒的直径约为0.000043毫米,则0.000043用科学记数法表示()
A. 0.43×10-4B. 43x105C. 4.3x10-4D. 4.3×10-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+3)(x+n)=x2+mx-15,则m的值为( )
A. -2B. 2C. 5D. -5
相关试题

