【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连结CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
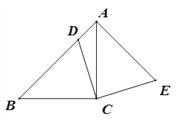
(1)求证:AB⊥AE;
(2)若![]() ,求证:四边形ADCE为正方形.
,求证:四边形ADCE为正方形.
参考答案:
【答案】证明:(1)∵∠ACB=90°,AC=BC,
∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,
∴∠DCE=90°,CD=CE,
∵∠ACB=90°,
∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,
即∠BCD=∠ACE,
在△BCD和△ACE中
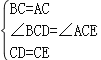 ,
,
∴△BCD≌△ACE,
∴∠B=∠CAE=45°,
∴∠BAE=45°+45°=90°,
∴AB⊥AE;
(2)∵![]() ,
,
而BC=AC,
∴![]() ,
,
∵∠DAC=∠CAB,
∴△DAC∽△CAB,
∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,
∴四边形ADCE为矩形,
∵CD=CE,
∴四边形ADCE为正方形
【解析】试题分析:(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论;
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形.
解答:证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°,
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE,
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE,
在△BCD和△ACE中,∵BC=AC,∠BCD=∠ACE,CD=CE,∴△BCD≌△ACE,
∴∠B=∠CAE=45°,∴∠BAE=45°+45°=90°,∴AB⊥AE;
(2)∵BC2=ADAB,而BC=AC,∴AC2=ADAB,
∵∠DAC=∠CAB,∴△DAC∽△CAB,∴∠CDA=∠BCA=90°,
而∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形,
∵CD=CE,∴四边形ADCE为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:

(1)作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;
(2)点B1的坐标为 , 点C2的坐标为 -
科目: 来源: 题型:
查看答案和解析>>【题目】若实数x满足等式(x+4)3=﹣27,则x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“水是生命之源”,某城市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月
单价(元/m3)
不超过20m3
2.8
超过20m3的部分
3.8
另:每立方米用水加收0.2元的城市污水处理费
(1)如果1月份某用户用水量为19m3 , 那么该用户1月份应该缴纳水费元.
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=4(x﹣3)2+7,开口_____,对称轴为_____,顶点坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
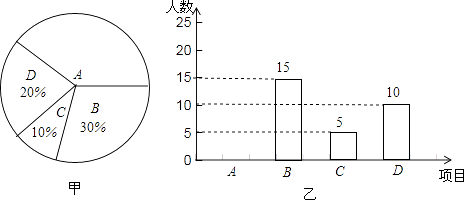
(1)样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;
(2)请把条形统计图补充完整;
(3)若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
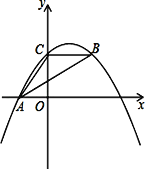
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
相关试题

