【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相较于点D,E,F,且BF=BC,⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH. 
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HGHB的值.
参考答案:
【答案】
(1)证明:∵∠ABC=90°,
∴∠EBF=90°,
∵DF⊥AC,
∴∠ADF=90°,
∴∠C+∠A=∠A+∠AFD=90°,
∴∠C=∠BFE,
在△ABC与△EBF中, 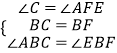 ,
,
∴△ABC≌△EBF
(2)BD与⊙O相切,如图1,连接OB
证明如下:∵OB=OF,
∴∠OBF=∠OFB,
∵∠ABC=90°,AD=CD,
∴BD=CD,
∴∠C=∠DBC,
∵∠C=∠BFE,
∴∠DBC=∠OBF,
∵∠CBO+∠OBF=90°,∴∠DBC+∠CBO=90°,
∴∠DBO=90°,
∴BD与⊙O相切
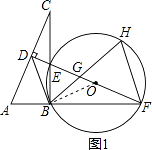
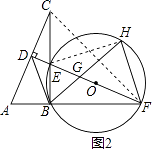
(3)解:如图2,连接CF,HE,
∵∠CBF=90°,BC=BF,
∴CF= ![]() BF,
BF,
∵DF垂直平分AC,
∴AF=CF=AB+BF=1+BF= ![]() BF,
BF,
∴BF= ![]() +1,
+1,
∵△ABC≌△EBF,
∴BE=AB=1,
∴EF= ![]() =
= ![]() ,
,
∵BH平分∠CBF,
∴ ![]() ,
,
∴EH=FH,
∴△EHF是等腰直角三角形,
∴HF= ![]() EF=
EF= ![]() ,
,
∵∠EFH=∠HBF=45°,∠BHF=∠BHF,
∴△BHF∽△FHG,
∴ ![]() ,
,
∴HGHB=HF2=2+ ![]() .
.
【解析】(1)由垂直的定义可得∠EBF=∠ADF=90°,于是得到∠C=∠BFE,从而证得△ABC≌△EBF;(2)BD与⊙O相切,如图1,连接OB证得∠DBO=90°,即可得到BD与⊙O相切;(3)如图2,连接CF,HE,有等腰直角三角形的性质得到CF= ![]() BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF=
BF,由于DF垂直平分AC,得到AF=CF=AB+BF=1+BF= ![]() BF,求得BF=
BF,求得BF= ![]() +1,有勾股定理解出EF
+1,有勾股定理解出EF ![]() =
= ![]() ,推出△EHF是等腰直角三角形,求得HF=
,推出△EHF是等腰直角三角形,求得HF= ![]() EF=
EF= ![]() ,通过△BHF∽△FHG,列比例式即可得到结论.
,通过△BHF∽△FHG,列比例式即可得到结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,不正确的是( )
A. 一个数与它的倒数的积是1
B. 一个数的绝对值与它的相反数的商是

C. 两个数的商为
 ,这两个数互为相反数
,这两个数互为相反数D. 两个数的积为1,这两个数互为倒数
-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级进行数学竞赛,在第二环节的10道题中,答对1题得10分,答错一题扣5分,不答不得分,二班实际得分
 分,则下列选项正确的是( )
分,则下列选项正确的是( )A. 答对1题,答错5题,不答4题 B. 答对2题,答错5题,不答3题
C. 答对2题,答错5题,不答3题 D. 答对4题,答错5题,不答1题
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)

(3)

(4)

(5)

(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)探究规律:如图,已知□ABCD,试用三种方法将它分成面积相等的两部分:



(2)解决问题:兄弟俩共同承包的一块平行四边形的土地,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了,聪明的你能帮他们解决这个问题吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”.
(1)求函数y=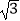 x+2的图象上所有“中国结”的坐标;
x+2的图象上所有“中国结”的坐标;
(2)若函数y=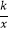 (k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图象上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=(k2﹣3k+2)x2+(2k2﹣4k+1)x+k2﹣k(k为常数)的图象与x轴相交得到两个不同的“中国结”,试问该函数的图象与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”? -
科目: 来源: 题型:
查看答案和解析>>【题目】一辆货车为一家摩托车配件批发部送货,先向南走了8km到达“华能”修理部,又向北走了3.5km到达“捷速”修理部,继续向北走了7.5km到达“志远”修理部,最后又回到了批发部.
(1)以批发部为原点,以向南的方向为正方向,用1个单位长度表示1km,你能在数轴上表示出“华能”、“捷速”、“志远”三家修理部的位置吗?
(2)“志远”修理部到“捷速”修理部多远?
(3)货车若行驶1千米需耗油0.5升,本次这辆货车共耗油多少升?
相关试题

