【题目】如图,把RI△ABC放在直角坐标系内,其中∠CAB=90°, BC=5.点A,B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线 ![]() 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
A.4
B.8
C.16
D.![]()
参考答案:
【答案】C
【解析】如图:

∵点A、B的坐标分别为(1,0)、(4,0),
∴AB=3,BC=5,
∵∠CAB=90
∴AC=4,
∴点C的坐标为(1,4),当点C落在直线y=2x﹣6上时,
∴令y=4,得到4=2x﹣6,解得x=5,
∴平移的距离为5﹣1=4,
∴线段BC扫过的面积为4×4=16,
故答案为:C.
三角形平移后,点C的横坐标改变,纵坐标不变,根据点c在直线y=2x-6上可求出点c的坐标,得出图形平移的距离,直线BC扫过的图形是一个平行四边形,再根据平行四边形面积公式求出结果。
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用二元一次方程组解应用题:甲、乙两地相距
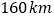 ,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行,
,一辆汽车和一辆拖拉机同时由两地以各自的速度匀速相向而行, 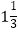 小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留
小时后相遇.相遇后,拖拉机以其原速继续前进,汽车在相遇处停留 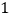 小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程?
小时后调转车头以其原速返回,在汽车再次出发半小时追上拖拉机.这时,汽车、拖拉机各自走了多少路程? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数中,不是无理数的是( )
A.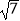
B.0.5
C.2π
D.0.151151115…(两个5之间依次多1个1) -
科目: 来源: 题型:
查看答案和解析>>【题目】《函数的图象与性质》拓展学习片段展示:
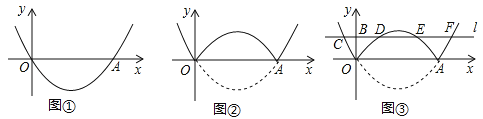
【问题】如图①,在平面直角坐标系中,抛物线y=a(x﹣2)2﹣
 经过原点O,与x轴的另一个交点为A,则a= .
经过原点O,与x轴的另一个交点为A,则a= .【操作】将图①中抛物线在x轴下方的部分沿x轴折叠到x轴上方,将这部分图象与原抛物线剩余部分的图象组成的新图象记为G,如图②.直接写出图象G对应的函数解析式.
【探究】在图②中,过点B(0,1)作直线l平行于x轴,与图象G的交点从左至右依次为点C,D,E,F,如图③.求图象G在直线l上方的部分对应的函数y随x增大而增大时x的取值范围.
【应用】P是图③中图象G上一点,其横坐标为m,连接PD,PE.直接写出△PDE的面积不小于1时m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:32﹣20170+tan45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).

(1)当点Q在边AC上时,正方形DEFQ的边长为 cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
-
科目: 来源: 题型:
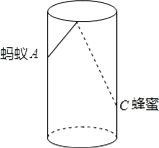
查看答案和解析>>【题目】如图,圆柱形玻璃杯,高为11cm,底面周长为16cm,在杯内离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为 . (结果保留根号)
相关试题

