【题目】解下列方程组:
(1)![]() (用代入法)
(用代入法)
(2)![]() (用加减法)
(用加减法)
(3)![]()
(4)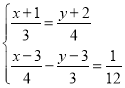 .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)利用代入法解二元一次方程组;
(2)利用加减法解二元一次方程组;
(3)先整理方程组,再用加减法解解二元一次方程组;
(4)先整理方程组,再用加减法解解二元一次方程组;
(1)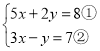
由②得:y=3x7③,
把③代入①得:5x+6x14=8,
解得:x=2,
把x=2代入③得:y=1,
则方程组的解为![]() ;
;
(2)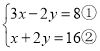
①+②得:4x=24,即x=6,
把x=6代入②得:y=5,
则方程组的解为![]() ;
;
(3)方程组整理得: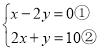
①+②×2得:5x=20,即x=4,
把x=4代入①得:y=2,
则方程组的解为![]() ;
;
(4)方程组整理得: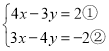 .
.
②×3①×4得:7x=14,即x=2,
把x=2代入①得:y=2,
则方程组的解为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
已知在Rt△ABC中,∠BAC=90°,AB=AC=2
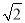 .
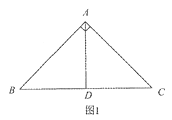
.(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
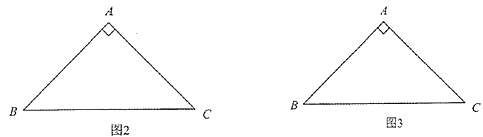
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
-
科目: 来源: 题型:
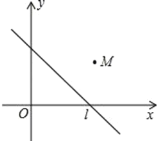
查看答案和解析>>【题目】如图,已知点 M 的坐标为(4,3),点 M 关于直线 l:y=﹣x+b 的对称点落在坐标轴上,则 b的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一节数学课上,老师出示了这样一个问题让学生探究:
已知:如图在△ABC中,点D 是BA边延长线上一动点,点F 在BC上,且
 ,连接DF交AC于点E .
,连接DF交AC于点E . (1)如图1,当点E恰为DF的中点时,请求出
 的值;
的值;(2)如图2,当
 时,请求出
时,请求出 的值(用含a的代数式表示).
的值(用含a的代数式表示).思考片刻后,同学们纷纷表达自己的想法:
甲:过点F作FG∥AB交AC于点G,构造相似三角形解决问题;
乙:过点F作FG∥AC交AB于点G,构造相似三角形解决问题;
丙:过点D作DG∥BC交CA延长线于点G,构造相似三角形解决问题;
老师说:“这三位同学的想法都可以” .
请参考上面某一种想法,完成第(1)问的求解过程,并直接写出第(2)问
 的值.
的值. 

图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求一次函数y=2x-2的图象l1与y=
 x-1的图象l2的交点P的坐标.
x-1的图象l2的交点P的坐标.(2)求直线
 与
与 轴交点A的坐标; 求直线
轴交点A的坐标; 求直线 与x轴的交点B的坐标;
与x轴的交点B的坐标;(3)求由三点P、A、B围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
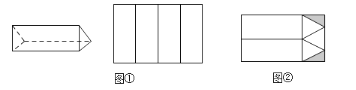
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
相关试题

