搜索
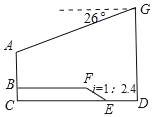
【题目】今年，重庆被“抖音”抖成了“网红城市”，其中解放碑的游客数量明显高于去年同期，如图，小冉和小田决定用所学知识测量解放碑AB的高度，按照以下方式合作并记录所得数据：小冉从大厦DG的底端D点出发，沿直线步行10.2米到达E点，再沿坡度i=1：2.4的斜坡EF行走5.2米到达F点，最后沿直线步行30米到达解放碑底部B点，小田从大厦DG的底端乘直行电梯上行到离D点51.5米的顶端G点，从G点观测到解放碑顶端A点的俯角为26°，若A，B，C，D，E，F，G在同一平面内，且B，F和C，E，D分别在同一水平线上，则解放碑AB的高度约为（ ）米．（精确到0.1米，参考数据：sin26°≈0.44，cos26°≈.90，tan26°≈0.49）
A. 29.0 B. 28.5 C. 27.5 D. 27.0
参考答案：
【答案】C
【解析】
作GH⊥BA于H，FM⊥CD于M．想办法求出BC、AH即可解决问题；
解：作GH⊥BA于H，FM⊥CD于M．则四边形BCMF，四边形CDGH是矩形．
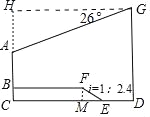
在Rt△FEM中，FM：EM=1：2.4，EF=5.2m，
∴FM=BC=2m，EM=4.8m，CM=BF=30m，
∴CD=CM+EM+DE=45m，
∴GH=CD=45m，
在Rt△AGH中，AH=GHtan26°≈22.05m，
∵CH=DG=51.5m，
∴AB=CH﹣BC﹣AH=51.5﹣2﹣22.05≈27.5（m），
故选：C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC为等边三角形，O为BC的中点，D、E分别在边AB、AC上．如图1．
（1）若∠DOE=120°，求证：OD=OE；
（2）如图2，BD=4，CE=2，M是DE的中点，求OM的长．
-
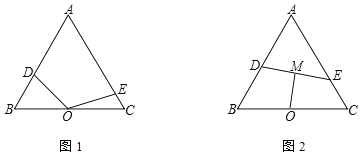
科目： 来源： 题型：
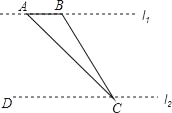
查看答案和解析>>【题目】如图，为了测量河对岸l1上两棵古树A、B之间的距离，某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点，测得∠ACB=15°，∠ACD=45°，若l1、l2之间的距离为50m，则A、B之间的距离为（ ）
A. 50m B. 25m C. （50﹣
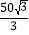）m D. （50﹣25
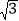）m -
科目： 来源： 题型：
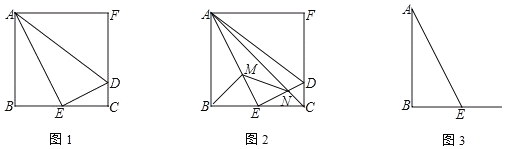
查看答案和解析>>【题目】已知：正方形ABCF中，E为BC中点，点D在CF上，AB=4，CD=1．
（1）判断△AED的形状，并证明；
（2）AC交DE于点N，M在AE上，且满足BM2﹣ME2=EN2﹣CN2，求证：BM⊥AC；
（3）若△APE是以AE为斜边的等腰直角三角形，直接写出BP的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】位于南开（融侨）中学旁边的“转转桥”是重庆市网红景点之一，在桥下人形天桥（如图1），其平面图如图2所示，天桥入口D点有一台阶DC，CD=0.5米，其坡度为i=1：0.75，在DC上方有一平层BC=1米，且BC与地面MN平行，在天桥顶端A点测得B点的俯角为63°，且AD⊥MN，为知道台阶AB的长度，请根据以上信息，帮小亮计算出台阶AB的长度，约为（ ）精确到0.1米，参考数据：sin63°≈0.90，cos63°≈0.45，tan63°≈2.00
A. 1.4米 B. 2.5米 C. 2.8米 D. 2.9米
-
科目： 来源： 题型：
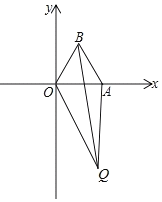
查看答案和解析>>【题目】在平面直角坐标系中，O(0，0)、B(a，b)，且a、b满足1﹣2a+a2+(b
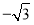)2=0．（1）求a，b的值；
（2）若点A在x轴正半轴上，且OA=2，在平面内有一动点Q(不在x轴上)，QO=m，QA=n，QB=p，且p2=m2+n2，求∠OQA的度数．
（3）阅读以下内容：对于实数a、b有(a﹣b)2≥0，∴a2﹣2ab+b2≥0，
即a2+b2≥2ab．
利用以上知识，在（2）的条件下求△AOQ的面积的最大值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠C=90°， ∠B=30°，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，又分别以M、N为圆心，大于
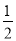MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D．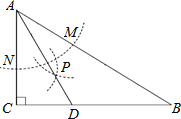
求证：（1）点D在AB的中垂线上．
（2）当CD=2时，求△ABC的面积．
相关试题
