【题目】在平面直角坐标系中,O(0,0)、B(a,b),且a、b满足1﹣2a+a2+(b![]() )2=0.
)2=0.
(1)求a,b的值;
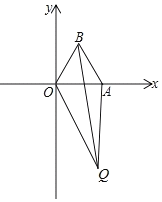
(2)若点A在x轴正半轴上,且OA=2,在平面内有一动点Q(不在x轴上),QO=m,QA=n,QB=p,且p2=m2+n2,求∠OQA的度数.
(3)阅读以下内容:对于实数a、b有(a﹣b)2≥0,∴a2﹣2ab+b2≥0,
即a2+b2≥2ab.
利用以上知识,在(2)的条件下求△AOQ的面积的最大值.
参考答案:
【答案】(1)a=1,b![]() ;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2
;(2)∠OQA的度数为30°或150°;(3)当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;当∠OQA=150°时,△AOQ的面积的最大值为2
;当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.
【解析】
(1)由题意根据完全平方式的非负性,即可求得a和b的值;
(2)根据题意易证△OAB为等边三角形,故可通过把△ABQ绕点A逆时针旋转60°得△AOC,把已知的QO=m、QA=n、QB=p统一到△OCQ中,得到△OCQ是直角三角形,再加上旋转得到的∠AQC=60°,即能求出∠OQA的度数;但由于不确定点Q的位置,故需分点Q在△OAB内部和点Q在△OAB外部两种情况讨论计算;
(3)由题意通过构造OQ边上的高AH求得△AOQ面积的表达式,根据条件给的不等式可知,当a=b时,ab可取得最大值为a2+b2,即OQ=AQ时,△AOQ取得最大值;根据勾股定理把AQ=OQ求出,即求出面积最大值;由于在(2)的条件下不确定∠OQA的度数,故需分两种情况讨论计算.
解:(1)∵1﹣2a+a2+(b![]() )2=0,
)2=0,
∴(1﹣a)2+(b![]() )2=0,
)2=0,
∴1﹣a=0,b![]() 0,
0,
∴a=1,b![]() .
.
(2)∵OA=2即A(2,0),B(1,![]() ),
),
∴OB![]() ,AB
,AB![]() ,
,
∴OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°,
把△ABQ绕点A逆时针旋转60°得△AOC,连接CQ,
∴∠CAQ=∠OAB=60°,AC=AQ=n,OC=BQ=p,
∴△ACQ是等边三角形,
∴CQ=AQ=n,∠AQC=60°,
∵p2=m2+n2即OC2=OQ2+CQ2,
∴△OCQ是直角三角形,∠OQC=90°,
①若点Q在△OAB的外部,如图1,
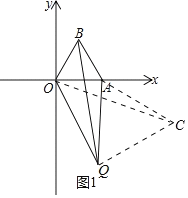
则∠OQA=∠OQC﹣∠AQC=90°﹣60°=30°;
②若点Q在△OAB的内部,如图2,
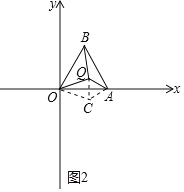
则∠OQA=∠OQC+∠AQC=90°+60°=150°,
综上所述:∠OQA的度数为30°或150°.
(3)∵a2+b2≥2ab,
∴当a=b时,a2+b2=2ab成立,即此时ab取得最大值,
过点A作AH⊥OQ于H,如图3,
∴∠AHQ=90°,
∵∠AQH=30°,
∴AH![]() AQ
AQ![]() n,
n,
∴S△AOQ![]() OQAH
OQAH![]() m
m![]() n
n![]() mn,
mn,
∴当m=n时,S△AOQ取得最大值![]() ,
,
①当∠OQA=30°时,如图3.
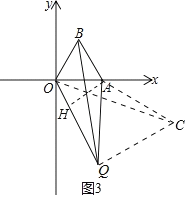
∵OQ=AQ=n,QH![]() ,
,
∴OH=OQ﹣QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ;
;
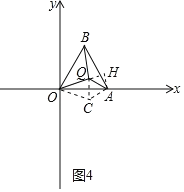
②当∠OQA=150°时,如图4,
∴OH=OQ+QH=n![]() n,
n,
∵OA=2,OA2=OH2+AH2,
∴(n![]() n)2+(
n)2+(![]() n)2=22,
n)2=22,
解得:n2=4(2![]() ),
),
∴S△AOQ![]() n2=2
n2=2![]() ,
,
综上所述:当∠OQA=30°时,△AOQ的面积的最大值为2![]() ;
;
当∠OQA=150°时,△AOQ的面积的最大值为2![]() .
.
-
科目: 来源: 题型:
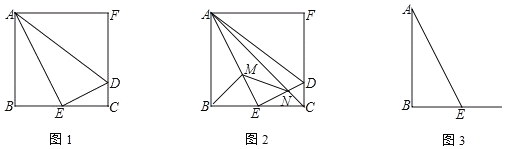
查看答案和解析>>【题目】已知:正方形ABCF中,E为BC中点,点D在CF上,AB=4,CD=1.
(1)判断△AED的形状,并证明;
(2)AC交DE于点N,M在AE上,且满足BM2﹣ME2=EN2﹣CN2,求证:BM⊥AC;
(3)若△APE是以AE为斜边的等腰直角三角形,直接写出BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,重庆被“抖音”抖成了“网红城市”,其中解放碑的游客数量明显高于去年同期,如图,小冉和小田决定用所学知识测量解放碑AB的高度,按照以下方式合作并记录所得数据:小冉从大厦DG的底端D点出发,沿直线步行10.2米到达E点,再沿坡度i=1:2.4的斜坡EF行走5.2米到达F点,最后沿直线步行30米到达解放碑底部B点,小田从大厦DG的底端乘直行电梯上行到离D点51.5米的顶端G点,从G点观测到解放碑顶端A点的俯角为26°,若A,B,C,D,E,F,G在同一平面内,且B,F和C,E,D分别在同一水平线上,则解放碑AB的高度约为( )米.(精确到0.1米,参考数据:sin26°≈0.44,cos26°≈.90,tan26°≈0.49)
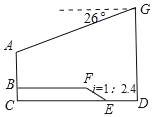
A. 29.0 B. 28.5 C. 27.5 D. 27.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】位于南开(融侨)中学旁边的“转转桥”是重庆市网红景点之一,在桥下人形天桥(如图1),其平面图如图2所示,天桥入口D点有一台阶DC,CD=0.5米,其坡度为i=1:0.75,在DC上方有一平层BC=1米,且BC与地面MN平行,在天桥顶端A点测得B点的俯角为63°,且AD⊥MN,为知道台阶AB的长度,请根据以上信息,帮小亮计算出台阶AB的长度,约为( )精确到0.1米,参考数据:sin63°≈0.90,cos63°≈0.45,tan63°≈2.00

A. 1.4米 B. 2.5米 C. 2.8米 D. 2.9米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°, ∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,又分别以M、N为圆心,大于
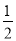 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.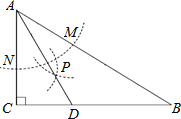
求证:(1)点D在AB的中垂线上.
(2)当CD=2时,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
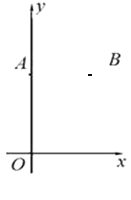
(1)只用直尺(没有刻度)和圆规,求作一个点P,使点P同时满足下列两个条件:
①点P到A,B两点的距离相等; ②点P到∠xOy的两边的距离相等.(要求保留作图痕迹,不必写出作法)
(2)在(1)作出点P后,点P的坐标为_________.
相关试题

