【题目】△ABC为等边三角形,O为BC的中点,D、E分别在边AB、AC上.如图1.
(1)若∠DOE=120°,求证:OD=OE;
(2)如图2,BD=4,CE=2,M是DE的中点,求OM的长.
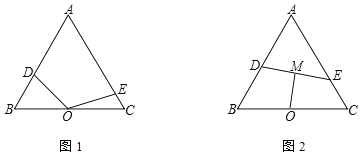
参考答案:
【答案】(1)证明见解析;(2)MO![]() .
.
【解析】
(1)根据题意以O为圆心,OD长为半径画弧,交AB于点H,连接OH,则OH=OD,根据△ABC为等边三角形,∠DOE=120°,可知∠OEC=∠ADO,则可证出△BHO≌△CEO,可得OH=OE,即OD=OE;
(2)由题意连接BE,取BE的中点G,连接MG并延长交BC于点H,连接GO,过点O作OJ垂直MH,M为DE中点,G为BE中点,则MG∥DB,MG=![]() DB,∠MHO=∠ABC=60°,点O为BC的中点,点G为BE的中点,则GO∥EC,GO=
DB,∠MHO=∠ABC=60°,点O为BC的中点,点G为BE的中点,则GO∥EC,GO=![]() EC=1,∠GOH=∠C=60°,可推出HG=HO=GO=1,GJ=
EC=1,∠GOH=∠C=60°,可推出HG=HO=GO=1,GJ=![]() ,OJ=
,OJ=![]() ,在Rt△MOJ中,(
,在Rt△MOJ中,(![]() )2+(
)2+(![]() )2=MO2,解得MO=
)2=MO2,解得MO=![]() .
.
解:(1)如图1所示,
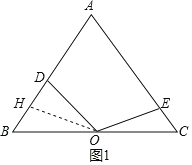
以O为圆心,OD长为半径画弧,交AB于点H,连接OH,则OH=OD.
∵△ABC为等边三角形,
∴∠B=∠C=∠A=60°,
∵∠DOE=120°,
∴∠A+∠DOE=180°,
∴∠ADO+∠AEO=180°,
∵∠OEC+∠AEO=180°,
∴∠OEC=∠ADO,
∵∠HDO=∠DHO,
∴∠BHO=∠ADO=∠OEC,
∵O为BC的中点,
∴BO=OC,
∴△BHO≌△CEO(AAS),
∴OH=OE,
∴OD=OE.
(2)如图2所示,
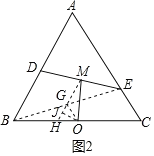
连接BE,取BE的中点G,连接MG并延长交BC于点H,连接GO,过点O作OJ垂直MH.
∵M为DE中点,G为BE中点,
∴MG∥DB,MG![]() DB=2,
DB=2,
∴∠MHO=∠ABC=60°,
∵点O为BC的中点,点G为BE的中点,
∴GO∥EC,GO![]() EC=1,
EC=1,
∴∠GOH=∠C=60°,
△GOH为等边三角形,
∴HG=HO=GO=1,
∴GJ![]() ,OJ
,OJ![]() ,
,
在Rt△MOJ中,
(![]() )2+(
)2+(![]() )2=MO2,
)2=MO2,
解得:MO![]() .
.
-
科目: 来源: 题型:
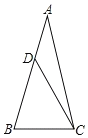
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=30°,点D在边AB上,∠ACD=15°,则
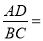 ____.
____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AH∥CG,且分别交对角线BD于H、G,连接CH和AG,求证:∠CHG=∠AGH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,tan∠BAC=2,A(0,a),B(b,0),点C在第二象限,BC与y轴交于点D(0,c),若y轴平分∠BAC,则点C的坐标不能表示为( )
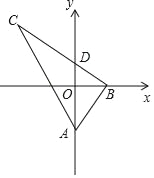
A. (b+2a,2b) B. (﹣b﹣2c,2b)
C. (﹣b﹣c,﹣2a﹣2c) D. (a﹣c,﹣2a﹣2c)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
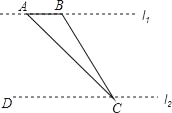
A. 50m B. 25m C. (50﹣
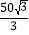 )m D. (50﹣25
)m D. (50﹣25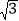 )m
)m -
科目: 来源: 题型:
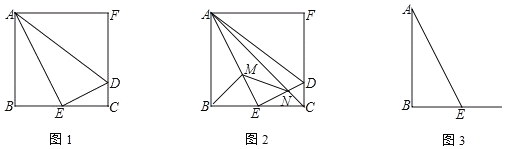
查看答案和解析>>【题目】已知:正方形ABCF中,E为BC中点,点D在CF上,AB=4,CD=1.
(1)判断△AED的形状,并证明;
(2)AC交DE于点N,M在AE上,且满足BM2﹣ME2=EN2﹣CN2,求证:BM⊥AC;
(3)若△APE是以AE为斜边的等腰直角三角形,直接写出BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,重庆被“抖音”抖成了“网红城市”,其中解放碑的游客数量明显高于去年同期,如图,小冉和小田决定用所学知识测量解放碑AB的高度,按照以下方式合作并记录所得数据:小冉从大厦DG的底端D点出发,沿直线步行10.2米到达E点,再沿坡度i=1:2.4的斜坡EF行走5.2米到达F点,最后沿直线步行30米到达解放碑底部B点,小田从大厦DG的底端乘直行电梯上行到离D点51.5米的顶端G点,从G点观测到解放碑顶端A点的俯角为26°,若A,B,C,D,E,F,G在同一平面内,且B,F和C,E,D分别在同一水平线上,则解放碑AB的高度约为( )米.(精确到0.1米,参考数据:sin26°≈0.44,cos26°≈.90,tan26°≈0.49)
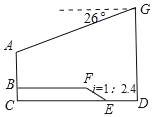
A. 29.0 B. 28.5 C. 27.5 D. 27.0
相关试题

