【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是 (填写序号)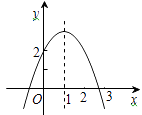
参考答案:
【答案】②③④
【解析】①∵抛物线的开口向下,∴a<0,
∵与y轴的交点为在y轴的正半轴上,∴c>0,
∵对称轴为x= ![]() >0,∴a、b异号,即b>0,
>0,∴a、b异号,即b>0,
∴abc<0;
故本结论错误;②从图象知,该函数与x轴有两个不同的交点,所以根的判别式△=b24ac>0;
故本结论正确;③∵对称轴为x= ![]() =1,
=1,
∴b=2a,
故本结论正确;④由图象知,x=1时y>2,所以a+b+c>2,故本结论正确.
故答案为②③④.
根据抛物线的开口方向、与y轴的交点情况可确定a、c的取值范围,根据对称轴在y轴的左侧,a、b同号;对称轴在y轴的右侧,a、b异号,即可对①作出判断;根据抛物线与x轴的交点个数,可对②作出判断;根据对称轴为直线x=1=-![]() ,可对③作出判断;由图像可知,当x=1时,函数值y最大,可对④作出判断;即可得出结论。
,可对③作出判断;由图像可知,当x=1时,函数值y最大,可对④作出判断;即可得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率 -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料,面市后果然供不应求,又用8100元购进这种饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若两次进饮料都按同一价格销售,两批全部售完后,获利不少于2700元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=
 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
相关试题

