【题目】如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y= ![]() 图象上.
图象上.
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
参考答案:
【答案】
(1)解:将A(1,5)和点B(m,1)代入y=![]() 得:
得:
m=5,k=5.
(2)解:设直AB所对应的一次函数关系式为:y=ax+b(a≠0),
将A(1,5)和点B(5,1)代入可得 ![]() ,
,
解得a=-1,b=6,
∴y=-x+6,
令y=0,得x=6,即OC=6,
S△AOC= ![]() OC×AE=
OC×AE= ![]() ×6×5=15.
×6×5=15.
【解析】(1)先将A(1,5)和点B(m,1)代入反比例函数解析式即可求出m、k的值。
(2)先根据A、B两点坐标求出直线AB的函数解析式,再根据y=0求出直线AB与x轴的交点C的坐标,根据三角形的面积公式即可求解。
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是直线x=1,有以下四个结论:
①abc>0;②b2-4ac>0;③b=-2a;④a+b+c>2.其中正确的是 (填写序号)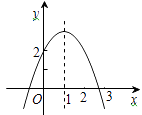
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】(列二元一次方程组解应用题)某公司共有3个一样规模的大餐厅和2个一样规模的小餐厅,经过测试同时开放2个大餐厅和1个小餐厅,可供300名员工就餐;同时开放1个大餐厅,1个小餐厅,可供170名员工就餐.
(1)请问1个大餐厅、1个小餐厅分别可供多少名员工就餐;
(2)如果3个大餐厅和2个小餐厅全部开放,那么能否供全体450名员工就餐?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
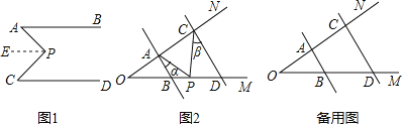
-
科目: 来源: 题型:
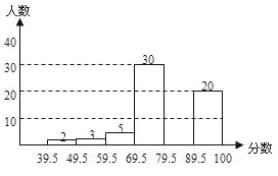
查看答案和解析>>【题目】我市今年九年级体育考试结束后,从某县3000名参考学生中抽取了100名考生成绩进行统计分析(满分100分,记分均为整数),得到如图所示的频数分布直方图,请你根据图形完成下列问题:
(1)本次抽样的样本容量是_________
(2)请补全频数分布直方图.
(3)若80分以上(含80分)为优秀,请你据此估算该县本次考试的优秀人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
相关试题

