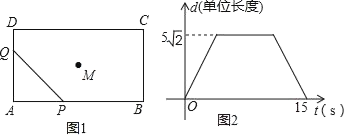
【题目】如图1已知矩形![]() ,
,![]() ,点
,点![]() 为矩形中心(
为矩形中心(![]() 与
与![]() 交点),现有两动点
交点),现有两动点![]() 分别沿着
分别沿着![]() 及
及![]() 的方向同时出发匀速运动,速度都为每秒一个单位长度,当点
的方向同时出发匀速运动,速度都为每秒一个单位长度,当点![]() 到达终点
到达终点![]() 时两动点都停止运动,连接
时两动点都停止运动,连接![]() ,在运动过程中,设运动时间为
,在运动过程中,设运动时间为![]() ,线段
,线段![]() 长度为
长度为![]() 个单位长度,
个单位长度,![]() 与
与![]() 的函数关系如图2
的函数关系如图2
(1)![]()
![]() .
.
(2)![]() 为多少时,线段
为多少时,线段![]() 经过点
经过点![]() ?并且求出此时
?并且求出此时![]() 的度数.
的度数.
(3)运动过程中,连接![]() 和
和![]() ,求当
,求当![]() 为直角时的
为直角时的![]() 值.
值.
参考答案:
【答案】(1)5,10;(2)![]() ,
,![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 为直角.
为直角.
【解析】
(1)利用图中信息,可知当点Q到达点D时,![]() ,即可推出AD=5,观察图象可知:点P在线段AB上的运动时间为10s,由此即可求出AB的长;
,即可推出AD=5,观察图象可知:点P在线段AB上的运动时间为10s,由此即可求出AB的长;
(2)易知:当DQ=PB时,PQ经过点M.由此构建方程即可解决问题;
(3)只要证明∠AMP=∠AMQ=45°,设PH=MH=a,则AH=2a,由此构建方程即可解决问题.
(1)由题意:当点![]() 到达点
到达点![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
观察图象可知:点![]() 在线段
在线段![]() 上的运动时间为
上的运动时间为![]() ,
,
![]() ,
,
故答案为5,10.
(2)如图3中,
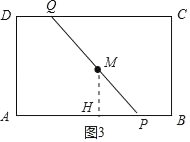
易知:当![]() 时,
时,![]() 经过点
经过点![]() .
.
则有:![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() .
.
(3)如图4中,作![]() 于
于![]() .
.
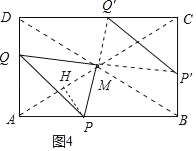
![]() ,
,
![]() 四点共圆,
四点共圆,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,此时
,此时![]() ,
,
根据对称性可知,当![]() 时,
时,![]() ,
,
![]() ,
,
综上所述,当![]() 或
或![]() 时,
时,![]() 为直角.
为直角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知
中,已知 和
和 的顶点坐标分别为
的顶点坐标分别为 、
、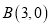 、
、 、
、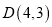 、
、 、
、 .
.按下列要求画图:以点
 为位似中心,将
为位似中心,将 向
向 轴左侧按比例尺
轴左侧按比例尺 放大得
放大得 的位似图形
的位似图形 ,并解决下列问题:
,并解决下列问题:(1)顶点
 的坐标为 ,
的坐标为 ,  的坐标为 ,
的坐标为 , 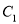 的坐标为 ;
的坐标为 ;(2)请你利用旋转、平移两种变换,使
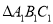 通过变换后得到
通过变换后得到 ,且
,且 恰与
恰与 拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
拼接成一个平行四边形 (非正方形).写出符合要求的变换过程.
-
科目: 来源: 题型:
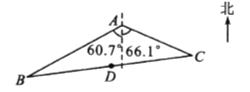
查看答案和解析>>【题目】如图,湿地景区岸边有三个观景台
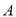 、
、 、
、 .已知
.已知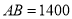 m,
m, 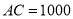 m,点
m,点 位于点
位于点 的南偏西60. 7°方向,点
的南偏西60. 7°方向,点 位于点
位于点 的南偏东66. 1°方向.
的南偏东66. 1°方向.(1)求
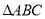 的面积;
的面积;(2)景区规划在线段
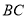 的中点
的中点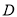 处修建一个湖心亭,并修建观景栈道
处修建一个湖心亭,并修建观景栈道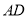 .试求
.试求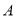 、
、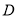 间的距离.(结果精确到0. 1 m,参考数据:
间的距离.(结果精确到0. 1 m,参考数据: 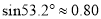 ,
, 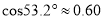 ,
, 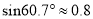 ,
, 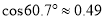 ,
, 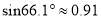 ,
,  ,
, 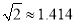 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长度为5的动线段
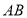 分别与坐标系横轴、纵轴的正半轴交于点
分别与坐标系横轴、纵轴的正半轴交于点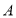 、点
、点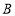 ,点
,点 和点
和点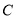 关于
关于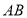 对称,连接
对称,连接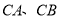 ,过点
,过点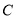 作
作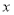 轴的垂线段
轴的垂线段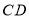 ,交
,交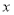 轴于点
轴于点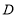
(1)移动点
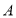 ,发现在某一时刻,
,发现在某一时刻,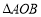 和以点
和以点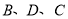 为顶点的三角形相似,求这一时刻点
为顶点的三角形相似,求这一时刻点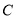 的坐标;
的坐标;(2)移动点
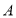 ,当
,当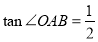 时求点
时求点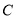 的坐标.
的坐标.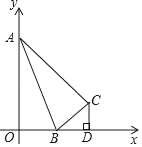
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
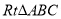 内接于⊙
内接于⊙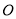 ,
, 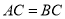 ,
, 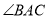 的平分线
的平分线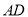 与⊙
与⊙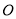 交于点
交于点 ,与
,与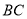 交于点
交于点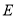 ,延长
,延长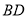 ,与
,与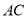 的延长线交于点
的延长线交于点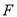 ,连接
,连接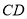 ,
,  是
是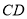 的中点,连接
的中点,连接 .
.(1)判断
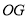 与
与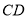 的位置关系,写出你的结论并证明;
的位置关系,写出你的结论并证明;(2)求证:
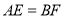 ;
;(3)若
 ,求⊙
,求⊙ 的面积.
的面积.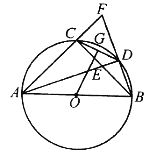
相关试题

