【题目】如图,在△ABC中,∠C=90°,AC=3,BC=4,点D,E分别在AC,BC上(点D与点A,C不重合),且∠DEC=∠A,将△DCE绕点D逆时针旋转90°得到△DC′E′.当△DC′E′的斜边、直角边与AB分别相交于点P,Q(点P与点Q不重合)时,设CD=x,PQ=y. 
(1)求证:∠ADP=∠DEC;
(2)求y关于x的函数解析式,并直接写出自变量x的取值范围.
参考答案:
【答案】
(1)证明:如图1中,
∵∠EDE′=∠C=90°,
∴∠ADP+∠CDE=90°,∠CDE+∠DEC=90°,
∴∠ADP=∠DEC.
(2)解:如图1中,
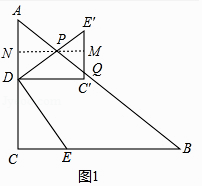
当C′E′与AB相交于Q时,即 ![]() <x≤
<x≤ ![]() 时,过P作MN∥DC′,设∠B=α
时,过P作MN∥DC′,设∠B=α
∴MN⊥AC,四边形DC′MN是矩形,
∴PM=PQcosα= ![]() y,PN=
y,PN= ![]() ×
× ![]() (3﹣x),
(3﹣x),
∴ ![]() (3﹣x)+
(3﹣x)+ ![]() y=x,
y=x,
∴y= ![]() x﹣
x﹣ ![]() ,
,
当DC′交AB于Q时,即 ![]() <x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,
<x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,
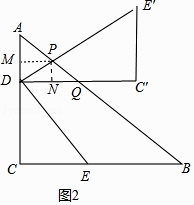
∴PN=DM,
∵DM= ![]() (3﹣x),PN=PQsinα=
(3﹣x),PN=PQsinα= ![]() y,
y,
∴ ![]() (3﹣x)=
(3﹣x)= ![]() y,
y,
∴y=﹣ ![]() x+
x+ ![]() .
.
综上所述,y= 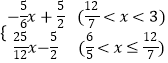
【解析】(1)根据等角的余角相等即可证明;(2)分两种情形①如图1中,当C′E′与AB相交于Q时,即 ![]() <x≤
<x≤ ![]() 时,过P作MN∥DC′,设∠B=α.②当DC′交AB于Q时,即
时,过P作MN∥DC′,设∠B=α.②当DC′交AB于Q时,即 ![]() <x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,分别求解即可;
<x<3时,如图2中,作PM⊥AC于M,PN⊥DQ于N,则四边形PMDN是矩形,分别求解即可;
【考点精析】本题主要考查了函数关系式和解直角三角形的相关知识点,需要掌握用来表示函数关系的数学式子叫做函数解析式或函数关系式;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产25个零件,现在生产600个零件所需时间与原计划生产450个零件所需时间相同,原计划平均每天生产多少个零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,双曲线y=
 经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5.
经过ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,SABCD=5. 
(1)填空:点A的坐标为;
(2)求双曲线和AB所在直线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.

(1)求证:BD=BE;
(2)若DE=2,BD= ,求CE的长.
,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD的对角线AC,BD相交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.

(1)填空:∠BAD与∠ACB的数量关系为;
(2)求 的值;
的值;
(3)将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD= ,求PC的长.
,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0,
 )
)
(1)若此抛物线经过点B(2,﹣ ),且与x轴相交于点E,F.
),且与x轴相交于点E,F.
①填空:b=(用含a的代数式表示);
(2)若a= ,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.
,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,
 )三点.
)三点.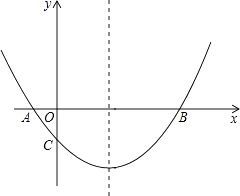
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
相关试题

