【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() )
)
(1)若此抛物线经过点B(2,﹣ ![]() ),且与x轴相交于点E,F.
),且与x轴相交于点E,F.
①填空:b=(用含a的代数式表示);
(2)若a= ![]() ,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.
,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.
参考答案:
【答案】
(1)[ "﹣2a﹣1
②当EF2的值最小时,求抛物线的解析式;
解:由①可得抛物线解析式为y=ax2﹣(2a+1)x+ ![]() ,
,
令y=0可得ax2﹣(2a+1)x+ ![]() =0,
=0,
∵△=(2a+1)2﹣4a× ![]() =4a2﹣2a+1=4(a﹣
=4a2﹣2a+1=4(a﹣ ![]() )2+
)2+ ![]() >0,
>0,
∴方程有两个不相等的实数根,设为x1、x2 ,
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴EF2=(x1﹣x2)2=(x1+x2)2﹣4x1x2= ![]() =(
=( ![]() ﹣1)2+3,
﹣1)2+3,
∴当a=1时,EF2有最小值,即EF有最小值,
∴抛物线解析式为y=x2﹣3x+ ![]() (2)
(2)
解:当a= ![]() 时,抛物线解析式为y=
时,抛物线解析式为y= ![]() x2+bx+
x2+bx+ ![]() ,
,
∴抛物线对称轴为x=﹣b,
∴只有当x=0、x=1或x=﹣b时,抛物线上的点才有可能离x轴最远,
当x=0时,y= ![]() ,当x=1时,y=
,当x=1时,y= ![]() +b+
+b+ ![]() =2+b,当x=﹣b时,y=
=2+b,当x=﹣b时,y= ![]() (﹣b)2+b(﹣b)+
(﹣b)2+b(﹣b)+ ![]() =﹣
=﹣ ![]() b2+
b2+ ![]() ,
,
①当|2+b|=3时,b=1或b=﹣5,且顶点不在0<x<1范围内,满足条件;
②当|﹣ ![]() b2+
b2+ ![]() |=3时,b=±3,对称轴为直线x=±3,不在0<x<1范围内,故不符合题意,
|=3时,b=±3,对称轴为直线x=±3,不在0<x<1范围内,故不符合题意,
综上可知b的值为1或﹣5
【解析】解:(1.)①∵抛物线y=ax2+bx+c的开口向上,且经过点A(0, ![]() ),
),
∴c= ![]() ,
,
∵抛物线经过点B(2,﹣ ![]() ),
),
∴﹣ ![]() =4a+2b+
=4a+2b+ ![]() ,
,
∴b=﹣2a﹣1,
所以答案是:﹣2a﹣1;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.

(1)求证:BD=BE;
(2)若DE=2,BD= ,求CE的长.
,求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3,BC=4,点D,E分别在AC,BC上(点D与点A,C不重合),且∠DEC=∠A,将△DCE绕点D逆时针旋转90°得到△DC′E′.当△DC′E′的斜边、直角边与AB分别相交于点P,Q(点P与点Q不重合)时,设CD=x,PQ=y.

(1)求证:∠ADP=∠DEC;
(2)求y关于x的函数解析式,并直接写出自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,四边形ABCD的对角线AC,BD相交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.

(1)填空:∠BAD与∠ACB的数量关系为;
(2)求 的值;
的值;
(3)将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD= ,求PC的长.
,求PC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,
 )三点.
)三点.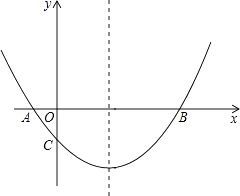
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )

A.∠2=35°
B.∠2=45°
C.∠2=55°
D.∠2=125° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①
 =
=  ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( ) 
A.①②③④
B.①④
C.②③④
D.①②③
相关试题

