【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0, ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;(2)P(2,﹣
;(2)P(2,﹣![]() );(3)点N的坐标为(4,﹣
);(3)点N的坐标为(4,﹣![]() ),(2+
),(2+![]() ,
, ![]() )或(2﹣
)或(2﹣![]() ,
, ![]() ).
).
【解析】试题分析:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),∵A(﹣1,0),B(5,0),C(0,![]() )三点在抛物线上,∴
)三点在抛物线上,∴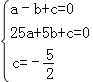 ,解得
,解得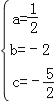 .∴抛物线的解析式为:y=
.∴抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ;
;
(2)∵抛物线的解析式为:y=![]() x2﹣2x﹣
x2﹣2x﹣![]() ,∴其对称轴为直线x=﹣
,∴其对称轴为直线x=﹣![]() =﹣
=﹣![]() =2,连接BC,如图1所示,
=2,连接BC,如图1所示,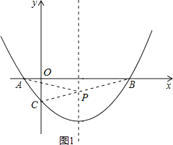
∵B(5,0),C(0,﹣![]() ),∴设直线BC的解析式为y=kx+b(k≠0),∴
),∴设直线BC的解析式为y=kx+b(k≠0),∴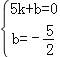 ,解得
,解得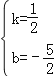 ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣
x﹣![]() ,当x=2时,y=1﹣
,当x=2时,y=1﹣![]() =﹣
=﹣![]() ,∴P(2,﹣
,∴P(2,﹣![]() );
);
(3)存在.如图2所示,
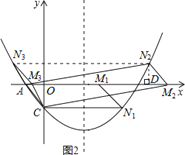
①当点N在x轴下方时,∵抛物线的对称轴为直线x=2,C(0,﹣![]() ),∴N1(4,﹣
),∴N1(4,﹣![]() );
);
②当点N在x轴上方时,如图2,过点N2作N2D⊥x轴于点D,在△AN2D与△M2CO中,
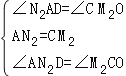 ∴△AN2D≌△M2CO(ASA),∴N2D=OC=
∴△AN2D≌△M2CO(ASA),∴N2D=OC=![]() ,即N2点的纵坐标为
,即N2点的纵坐标为![]() .∴
.∴![]() x2﹣2x﹣
x2﹣2x﹣![]() =
=![]() ,
,
解得x=2+![]() 或x=2﹣
或x=2﹣![]() ,∴N2(2+
,∴N2(2+![]() ,
,![]() ),N3(2﹣
),N3(2﹣![]() ,
,![]() ).综上所述,符合条件的点N的坐标为N1(4,﹣
).综上所述,符合条件的点N的坐标为N1(4,﹣![]() ),N2(2+
),N2(2+![]() ,
,![]() )或N3(2﹣
)或N3(2﹣![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图一,在平面直角坐标系中,
 是
是 轴正半轴上一点,
轴正半轴上一点, 是第四象限一点,
是第四象限一点, 轴,交
轴,交 轴负半轴于
轴负半轴于 ,且(a-2)+|b+3|=0,
,且(a-2)+|b+3|=0, 四边形AOBC=12.
四边形AOBC=12.(1)求
 点坐标
点坐标(2)如图二,设
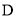 为线段
为线段 上一动点(点
上一动点(点 不与点
不与点 重合),求证:∠ADB+∠DBC-∠OAD=180°
重合),求证:∠ADB+∠DBC-∠OAD=180°(3)如图三,当
 点在线段
点在线段 上运动(点
上运动(点 不与点
不与点 重合),
重合), 点在线段
点在线段 上运动(点
上运动(点 不与点
不与点 重合)时,连接
重合)时,连接 、
、 作∠OAD、∠DEB的平分线交于
作∠OAD、∠DEB的平分线交于 点,请你探索∠AFE与∠ADE之间的关系,并说明理由.
点,请你探索∠AFE与∠ADE之间的关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.

(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8cm,BC=6cm.动点P、Q分别从点A、C以2cm/s的速度同时出发.动点P沿AB向终点B运动,动点Q沿CD向终点D运动,连结PQ交对角线AC于点O.设点P的运动时间为t(s).

(1)求OC的长.
(2)当四边形APQD是矩形时,直接写出t的值.
(3)当四边形APCQ是菱形时,求t的值.
(4)当△APO是等腰三角形时,直接写出t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )

A.7:20 B.7:30 C.7:45 D.7:50
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
 分别交坐标轴于
分别交坐标轴于 、
、 两点,直线上任意一点
两点,直线上任意一点 ,设点
,设点 到
到 轴和
轴和 轴的距离分别是
轴的距离分别是 和
和 ,则
,则 的最小值为( )
的最小值为( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

