Question

【题目】如图，在矩形ABCD中，AB=8cm，BC=6cm．动点P、Q分别从点A、C以2cm/s的速度同时出发．动点P沿AB向终点B运动，动点Q沿CD向终点D运动，连结PQ交对角线AC于点O．设点P的运动时间为t（s）．

（1）求OC的长．

（2）当四边形APQD是矩形时，直接写出t的值．

（3）当四边形APCQ是菱形时，求t的值．

（4）当△APO是等腰三角形时，直接写出t的值．

Answer 1

【答案】（1）5；（2）t=2；（3）；（4）或或

【解析】

（1）根据矩形的性质以及勾股定理判定≌，即可得解；

（2）根据题意判定当四边形APQD是矩形时，P、Q分别为AB、CD的中点，即可得解；

（3）根据菱形的性质以及勾股定理的运用，构建一元二次方程，即可得解；

（4）分情况：当AO=OP时，当AO=AP时，当AP=OP时，求解即可.

（1）∵四边形ABCD是矩形，

∴．

∴，．

在Rt△ABC中，∠B=90°，

由勾股定理，得．

∵，

∴≌．

∴．

（2）当四边形APQD是矩形时，P、Q分别为AB、CD的中点

即=4

t=2．

（3）如图，当四边形APCQ是菱形时，AP=CP=2t．

∴PB=8-2t．

在Rt△BCP中，∠B=90°，

由勾股定理，得．

∴．

解得．

当时，四边形APCQ是菱形．

（4）当AO=OP时，如图所示：

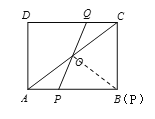
∵AO=5

∴P运动到点B

∴；

当AO=AP时，

∵AO=AP=5

∴；

当AP=OP时，

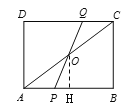
由（2），得OH=3，AH=4

∴PH=4-2t,OP=2t

∴，即

∴

综上所述，或或．