搜索
【题目】一般地，任何一个无限循环小数都可以写成分数形式，如0.
＝0.777…，它的循环节有一位，设0. ＝x，由0. ＝0777…，可知，10x＝7.777…，所以10x﹣x＝7，得x＝
．于是，得0. ＝，再如0.
＝0.737373…，它的循环节有两位，设0.＝x，由0.＝0.737373…可知，100x＝73.7373…，所以100x﹣x＝73．解方程得x＝
．于是，得0. ＝，类比上述方法，无限循环小数0. 3
化为分数形式为_____．
参考答案：
【答案】
【解析】
仿照给出的无限小数写成分数的方法，把无限循环小数
化为分数．
解：设无限循环小数＝x，则1000x＝735.735735…，
∴1000x﹣x＝735，
解方程，得x＝
＝
．
故答案为：．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某年5月，我国南方某省A、B两市遭受严重洪涝灾害，1.5万人被迫转移，邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后，决定调运物资支援灾区．已知C市有救灾物资240吨，D市有救灾物资260吨，现将这些救灾物资全部调往A、B两市．已知从C市运往A、B两市的费用分别为每吨20元和25元，从D市运往往A、B两市的费用分别为每吨15元和30元，设从C市运往B市的救灾物资为x吨．
（1）请填写下表；
A
B
合计（吨）
C
x
240
D
260
总计（吨）
200
300
500
（2）设C、D两市的总运费为W元，求W与x之间的函数关系式，并写出自变量x的取值范围；
（3）经过抢修，从C市到B市的路况得到了改善，缩短了运输时间，运费每吨减少n元（N＞0），其余路线运费不变，若C、D两市的总运费的最小值不小于10080元，求n的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列事件中是不可能事件的是（ ）
A. 任意画一个四边形，它的内角和是
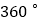
B. 若
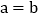，则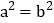
C. 一只不透明的袋子共装有3个小球，它们的标号分别为1、2、3，从中摸出一个小球，标号是“5”
D. 掷一枚质地均匀的硬币，落地时正面朝上
-
科目： 来源： 题型：
查看答案和解析>>【题目】中央电视台的《朗读者》节目激发了同学们的读书热情，为了引导学生“多读书，读好书”，某校对八年级部分学生的课外阅读量进行了随机调查，整理调查结果发现，学生课外阅读的本数量少的有
本，最多的有
本，并根据调查结果绘制了不完整的图表，如下所示：本数（本）
频数（人数）
频率
合计
（
）统计图表中的
__________，
__________，
__________．（
）请将频数分布直方图补充完整．（
）求所有被调查学生课外阅读的平均本数．（
）若该校八年级共有
名学生，请你估计该校八年级学生课外阅读本及以上的人数． -
科目： 来源： 题型：
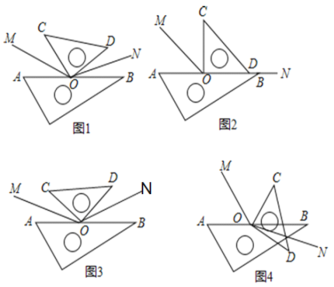
查看答案和解析>>【题目】综合与探究问题背景数学活动课上，老师将一副三角尺按图（1）所示位置摆放，分别作出∠AOC，∠BOD的平分线OM、ON，然后提出如下问题：求出∠MON的度数．
特例探究“兴趣小组”的同学决定从特例入手探究老师提出的问题，他们将三角尺分别按图2、图3所示的方式摆放，OM和ON仍然是∠AOC和∠BOD的角平分线．其中，按图2方式摆放时，可以看成是ON、OD、OB在同一直线上．按图3方式摆放时，∠AOC和∠BOD相等．
（1）请你帮助“兴趣小组”进行计算：图2中∠MON的度数为 °．图3中∠MON的度数为 °．
发现感悟
解决完图2，图3所示问题后，“兴趣小组”又对图1所示问题进行了讨论：
小明：由于图1中∠AOC和∠BOD的和为90°，所以我们容易得到∠MOC和∠NOD的和，这样就能求出∠MON的度数．
小华：设∠BOD为x°，我们就能用含x的式子分别表示出∠NOD和∠MOC度数，这样也能求出∠MON的度数．
（2）请你根据他们的谈话内容，求出图1中∠MON的度数．
类比拓展
受到“兴趣小组”的启发，“智慧小组”将三角尺按图4所示方式摆放，分别作出∠AOC、∠BOD的平分线OM、ON，他们认为也能求出∠MON的度数．
（3）你同意“智慧小组”的看法吗？若同意，求出∠MON的度数；若不同意，请说明理由．
-
科目： 来源： 题型：
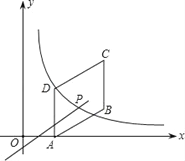
查看答案和解析>>【题目】如图，四边形ABCD是平行四边形，点A（1，0），B（4，1），C（4，3），反比例函数y=
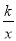的图象经过点D，点P是一次函数y=mx+3﹣4m（m≠0）的图象与该反比例函数图象的一个公共点；（1）求反比例函数的解析式；
（2）通过计算说明一次函数y=mx+3﹣4m的图象一定过点C；
（3）对于一次函数y=mx+3﹣4m（m≠0），当y随x的增大而增大时，确定点P的横坐标的取值范围，（不必写过程）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，函数
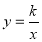的图象与函数
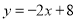的图象交于点
，
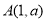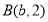.(1)求函数
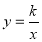的表达式；(2)观察图象，直接写出不等式
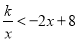的解集；(3)若点
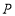是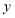
轴上的动点，当
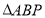周长最小时，求点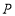的坐标.
相关试题
