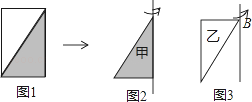
【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
参考答案:
【答案】(1)圆锥体,体积是376.8立方厘米;(2)空心的圆柱,体积为753.6立方厘米.
【解析】试题分析:(1)根据题干分析可得,分成的直角三角形的两条直角边分别是10厘米、6厘米,以较长边10厘米为轴旋转一周得到的是一个圆锥体,底面半径是6厘米,高是10厘米,据此利用圆锥的体积公式计算即可解答;
(2)根据题干分析可得,所形成的几何体的体积=底面半径是6厘米高是10厘米的圆柱体积﹣底面半径是6厘米高是10厘米的圆锥体积,据此利用圆柱和圆锥的体积公式计算即可解答.
试题解析:(1)根据题干分析可得:以其中一个直角三角形较长的直角边所在直线为轴,将纸板快速转动,可以形成一个圆锥体,
它的体积是![]() ×3.14×62×10=3.14×12×10=376.8(立方厘米).
×3.14×62×10=3.14×12×10=376.8(立方厘米).
(2)根据题干分析可得:乙三角形(如图3)旋转一周,可以形成一个挖去了等底等高圆锥的空心圆柱,
体积为:3.14×62×10-![]() ×3.14×62×10=3.14×360﹣3.14×120=3.14×240=753.6(立方厘米).
×3.14×62×10=3.14×360﹣3.14×120=3.14×240=753.6(立方厘米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】把弯曲的公路改直,就能够缩短路程可以用“_________”这一基本事实解释这一现象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数a,b在数轴上对应的A,B两点之间距离
 .
.探究运用
①数轴上表示1和3两点之间的距离是_____;数轴上表示x和2两点之间的距离是_____.
②根据图像比较大小:
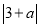 ______
______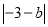 (填“<”、“=”、“>”).
(填“<”、“=”、“>”).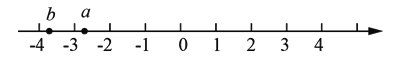
拓展延伸
③若点A.B、C在数轴上分别表示数-1、4、c,且点C到点A.B的距离之和是7,则c=_____.
④关于x的方程
 (m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
(m>n,k>0),借助数轴探究方程的解的情况,直接写出结论.
-
科目: 来源: 题型:
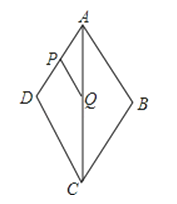
查看答案和解析>>【题目】如图,菱形ABCD,∠B=120°,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的面积为( )
A.6
B.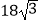
C.24
D.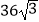
-
科目: 来源: 题型:
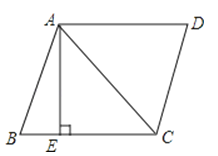
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
A.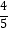
B.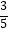
C.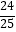
D.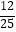
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+4a2=6a4
B.(a+1)2=a2+1
C.(a2)3=a5
D.x7÷x5=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.
(1)求二次函数
 的解析式;
的解析式;(2)将
 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线 ,直线y=m(m>0)交
,直线y=m(m>0)交 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);(3)在(2)的条件下,
 、
、 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与 、
、 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与 、
、 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
相关试题

