【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.

(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
试题分析:(1)根据待定系数法即可解决问题.
(2)先求出抛物线y2的顶点坐标,再求出其解析式,利用方程组以及根与系数关系即可求出MN.
(3)用类似(2)的方法,分别求出CD、EF即可解决问题.
试题解析:(1)∵二次函数![]() 过(﹣2,4),(﹣4,4)两点,∴
过(﹣2,4),(﹣4,4)两点,∴![]() ,解得:
,解得: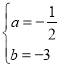 ,∴二次函数
,∴二次函数![]() 的解析式
的解析式![]() .
.
(2)∵![]() =
=![]() ,∴顶点坐标(﹣3,
,∴顶点坐标(﹣3,![]() ),∵将
),∵将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,∴抛物线
,∴抛物线![]() 的顶点坐标(﹣1,
的顶点坐标(﹣1,![]() ),∴抛物线
),∴抛物线![]() 为
为![]() ,由
,由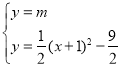 ,消去y整理得到
,消去y整理得到![]() ,设
,设![]() ,
,![]() 是它的两个根,则MN=
是它的两个根,则MN=![]() =
=![]() =
=![]() ;
;
(3)由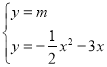 ,消去y整理得到
,消去y整理得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则CD=
,则CD=![]() =
=![]() =
=![]() ,由
,由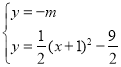 ,消去y得到
,消去y得到![]() ,设两个根为
,设两个根为![]() ,
,![]() ,则EF=
,则EF=![]() =
=![]() =
=![]() ,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
,∴EF=CD,EF∥CD,∴四边形CEFD是平行四边形.
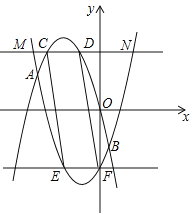
-
科目: 来源: 题型:
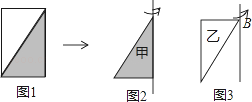
查看答案和解析>>【题目】如图1,把一张长10厘米、宽6厘米的长方形纸板分成两个相同的直角三角形.
(1)甲三角形(如图2)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
(2)乙三角形(如图3)旋转一周,可以形成一个怎样的几何体?它的体积是多少立方米?
-
科目: 来源: 题型:
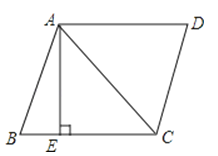
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
A.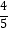
B.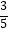
C.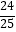
D.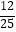
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a2+4a2=6a4
B.(a+1)2=a2+1
C.(a2)3=a5
D.x7÷x5=x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形AOCB在平面直角坐标系中的位置如图,若OA=2,∠AOC=45°,则B点的坐标是( )

A.(﹣2﹣ ,
,  )
)
B.(﹣2+ ,
,  )
)
C.(2+ ,
,  )
)
D.(2﹣ ,
,  )
) -
科目: 来源: 题型:
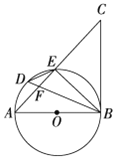
查看答案和解析>>【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
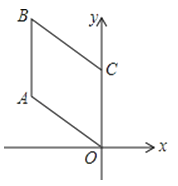
A.(﹣2,2+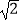 )
)
B.(2,2+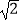 )
)
C.(-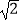 , 2+
, 2+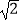 )
)
D.(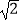 , 2+
, 2+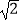 )
)
相关试题

