【题目】能用平方差公式计算的是( )
A.(-x+2y)(x-2y)B.(2x-y)(2y+x)C.(m-n)(n-m)D.![]()
参考答案:
【答案】D
【解析】
只要符合两项的和与这两项的差的积的形式,才能运用平方差公式计算.根据这个进行分析即可得到答案.
A. (x+2y)(x2y),因为x与x、2y与2y都是互为相反数,不符合平方差公式,所以不能运用平方差公式计算;
B. (2xy)(2y+x)=(2xy)(x+2y),括号里的相同字母的两项的系数的绝对值相等,不符合平方差公式,所以不能运用平方差公式计算;
C. (mn)(nm)=(mn)(m+n),因为m与m、n与n都是互为相反数,不符合平方差公式,所以不能运用平方差公式计算;
D. 99×101=(1001)(100+1)=100212=100001=9999,
符合平方差公式,所以能运用平方差公式计算;
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:
(1)y(x+y)+(x+y)(x-y)-x2,其中x=-2,y=
 ;
;(2)(x+y)2-2x(x+y),其中x=3,y=2.
(3)(a+b)2-2a(b+1)-a2b÷b,其中a=-2,b=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,
(1)写出A、B、C的坐标.
(2)以原点O为中心,将△ABC围绕原点O逆时针旋转180°得到△A1B1C1,画出△A1B1C1.
(3)求(2)中C到C1经过的路径以及OB扫过的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形。


(1)你认为图b中的阴影部分的正方形的边长等于__________________。
(2)请用两种不同的方法求图b中阴影部分的面积。
方法1:___________________________ 方法2:___________________________
(3)观察图b,你能写出下列三个代数式之间的等量关系吗?
代数式: (m+n)2 ,(m-n)2,mn
_______________________________________________________
(4)根据(3)题中的等量关系,解决如下问题:
若a+b=7,ab=5,求(a-b)2的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
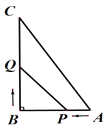
相关试题

