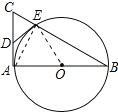
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
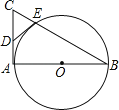
(1)若D为AC的中点,证明DE是⊙O的切线;
(2)若OA=![]() ,CE=1,求△ABC的面积.
,CE=1,求△ABC的面积.
参考答案:
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)连接AE,OE,∠AEB=90°,∠BAC=90°,在Rt△ACE中,D为AC的中点,则DE=AD=CD=![]() AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,则∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出结论;
(2)AB=2AO=2![]() ,由△BCA∽△BAE,得出
,由△BCA∽△BAE,得出![]() =
=![]() ,求出BE=3,BC=4,由勾股定理得AC=
,求出BE=3,BC=4,由勾股定理得AC=![]() =2,则S△ABC=
=2,则S△ABC=![]() ABAC代入即可得出结果.
ABAC代入即可得出结果.
(1)证明:连接AE,OE,如图所示:
∵AB是⊙O的直径,
∴∠AEB=90°,
∵AC是⊙O的切线,
∴∠BAC=90°,
∵在Rt△ACE中,D为AC的中点,
∴DE=AD=CD=![]() AC,
AC,
∴∠DEA=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,
∴OE⊥DE,
∵OE为半径,
∴DE是⊙O的切线;
(2)解:∵AO=![]() ,
,
∴AB=2AO=2![]() ,
,
∵∠CAB=∠AEB=90°,∠B=∠B,
∴△BCA∽△BAE,
∴![]() =
=![]() ,即AB2=BEBC=BE(BE+EC),
,即AB2=BEBC=BE(BE+EC),
∴(2![]() )2=BE2+BE,
)2=BE2+BE,
解得:BE=3或BE=﹣4(不合题意,舍去),
∴BE=3,
∴BC=BE+CE=3+1=4,
∴在Rt△ABC中,AC=![]() =
=![]() =2,
=2,
∴S△ABC=![]() ABAC=
ABAC=![]() ×2
×2![]() ×2=2
×2=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,该抛物线顶点为D,对称轴交x轴于点H.
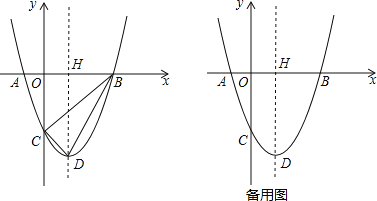
(1)求A,B两点的坐标;
(2)设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;
(3)以OB为边最第四象限内作等边△OBM.设点E为x轴的正半轴上一动点(OE>OH),连接ME,把线段ME绕点M顺时针旋转60°得MF,求线段DF的长的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.
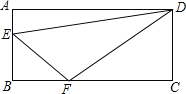
(1)当t为 时,△BEF为等腰直角三角形;
(2)当t为 时,△DFC为等腰直角三角形;
(3)是否存在某一时刻,使△EFB∽△FDC?若存在,求出t的值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣6x+c=0有一个根为2,则另一根为( )
A.2 B.3 C.4 D.8
-
科目: 来源: 题型:
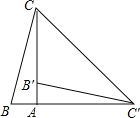
查看答案和解析>>【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左边到右边的变形是因式分解的是( )
A、(a+1)(a-1)=a2-1
B、a2-6a+9=(a-3)2
C、x2+2x+1=x(x+2)+1
D、-18x4y3=-6x2y2·3x2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式不能用平方差公式计算的是( )
A. (a+b)(a-b) B. (-a+b)(-a-b) C. (-a+b)(a-b) D. (a+b)( -a + b)
相关试题

