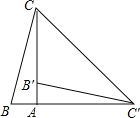
【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.
参考答案:
【答案】
【解析】
试题分析:根据旋转的性质可得△ABC≌△AB′C′,根据全等三角形的性质可得AC=AC′,∠B=∠AB′C′,则△ACC′是等腰直角三角形,然后根据三角形的外角的性质求得∠AB′C′即可.
解:由旋转的性质可得:△ABC≌△AB′C′,点B′在AC上,
∴AC=AC′,∠B=∠AB′C′.
又∵∠BAC=∠CAC′=90°,
∴∠ACC′=∠AC′C=45°.
∴∠AB′C′=∠ACC′+∠CC′B′=45°+30°=75°,
∴∠B=∠AB′C′=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.
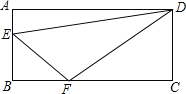
(1)当t为 时,△BEF为等腰直角三角形;
(2)当t为 时,△DFC为等腰直角三角形;
(3)是否存在某一时刻,使△EFB∽△FDC?若存在,求出t的值,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2﹣6x+c=0有一个根为2,则另一根为( )
A.2 B.3 C.4 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
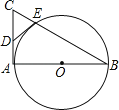
(1)若D为AC的中点,证明DE是⊙O的切线;
(2)若OA=
 ,CE=1,求△ABC的面积.
,CE=1,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式从左边到右边的变形是因式分解的是( )
A、(a+1)(a-1)=a2-1
B、a2-6a+9=(a-3)2
C、x2+2x+1=x(x+2)+1
D、-18x4y3=-6x2y2·3x2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式不能用平方差公式计算的是( )
A. (a+b)(a-b) B. (-a+b)(-a-b) C. (-a+b)(a-b) D. (a+b)( -a + b)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个图形成轴对称那么这两个图形一定是全等图形而两个全等图形_______成轴对称(填“一定”“一定不”或“不一定”)
相关试题

