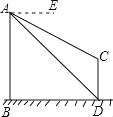
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
参考答案:
【答案】(1)两建筑物底部之间水平距离BD的长度为60米;
(2)建筑物CD的高度为(60﹣20![]() )米.
)米.
【解析】
试题分析:(1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
试题解析:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,在Rt△AFC中,∠FAC=30°,∴CF=AFtan∠FAC=60×![]() =20
=20![]() ,
,
又∵FD=60,∴CD=60﹣20![]() ,
,
∴建筑物CD的高度为(60﹣20![]() )米.
)米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:6a2-5a+3与5a2+2a -1的差,结果正确的是( )
A. a2-3a+4; B. a2-7a+4; C. a2-3a+2; D. a2-7a+2
-
科目: 来源: 题型:
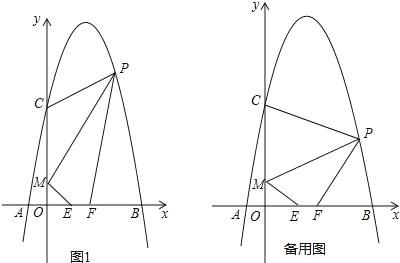
查看答案和解析>>【题目】如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在x=﹣4,﹣1,0,3中,满足不等式组
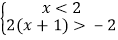 的x值是( )
的x值是( )
A.﹣4和0
B.﹣4和﹣1
C.0和3
D.﹣1和0 -
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式x2+ax+b分解因式,得(x+1)(x﹣3),则a,b的值分别是( )
A.a=﹣2,b=﹣3
B.a=2,b=3
C.a=﹣2,b=3
D.a=2,b=﹣3 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算不正确的是( )
A.(-1)2003=-1
B.-12002=1
C.(-1)2n=1(n为正整数)
D.(-1)2n+1=-1(n为正整数) -
科目: 来源: 题型:
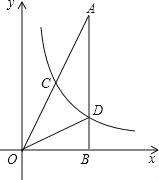
查看答案和解析>>【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=
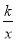 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.(1)求反比例函数解析式;
(2)求点C的坐标.
相关试题

