【题目】在平面直角坐标系中,A,B,C三点分别为(4,0),(4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP,垂足为P,则点P的坐标为_____.
参考答案:
【答案】(2,0)或(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0).
,0).
【解析】
先由已知得出D1(4,1),D2(4,﹣1),然后分类讨论D点的位置,分别利用相似三角形的性质和两点间距离公式求解即可.
解:∵A,B两点的坐标分别为(4,0),(4,4)
∴AB∥y轴
∵点D在直线AB上,DA=1
∴D1(4,1),D2(4,﹣1)
如图:
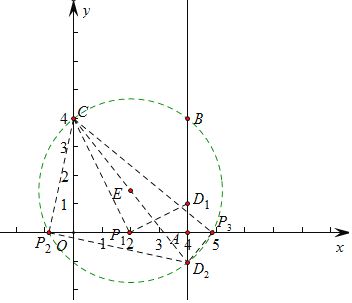
当点D在D1处,CP⊥DP时,
易得△COP1~△P1AD1,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:OP1=2,
∴P1(2,0);
当点D在D2处时,
∵C(0,4),D2(4,﹣1),
∴CD2的中点E为(2,![]() ),
),
∵CP⊥DP
∴点P为以E为圆心,CE长为半径的圆与x轴的交点,
设P(x,0),则PE=CE,即 =
=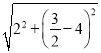 ,
,
解得:x=2±2![]() ,
,
∴P2(2﹣2![]() ,0),P3(2+2
,0),P3(2+2![]() ,0),
,0),
综上所述:点P的坐标为(2,0)或(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0),
,0),
故答案为:(2,0)或(2﹣2![]() ,0)或(2+2
,0)或(2+2![]() ,0).
,0).
-
科目: 来源: 题型:
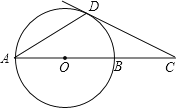
查看答案和解析>>【题目】如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为( )
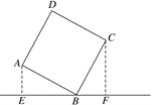
A. 5 B. 6 C. 9 D. 13
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
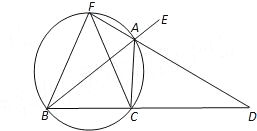
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 O
O 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线 和
和 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2( ,
,  ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
相关试题

