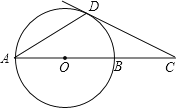
【题目】如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
参考答案:
【答案】120°;9.
【解析】
试题分析:可通过构建直角三角形来求解.连接OD,那么OD⊥CD,这时∠ADC=∠ADO+90°,我们不难发现∠ADO=∠A=30°,因此∠DC=120°;根据三角形的内角和,那么∠C=30°,直角三角形ODC中,有OD的长,∠C=30°,可求出OC的值,也就求出了AC的长.
试题解析:(1)连接OD,
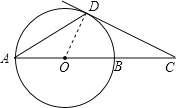
∵AO=OD,
∴∠ADO=∠DAO=30°,
∵CD是⊙O的切线,
∴∠CDO=90°,
∴∠ADC=∠ADO+∠CDO=30°+90°=120°;
(2)由(1)知∠COD=60°且OD=AO=![]() AB=3cm,
AB=3cm,
在Rt△COD中,∠C=30°,
∴OC=2OD=6cm,
∴AC=AO+OC=3+6=9cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)(问题解决)已知点
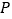 在
在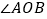 内,过点
内,过点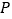 分别作关于
分别作关于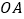 、
、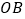 的对称点
的对称点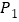 、
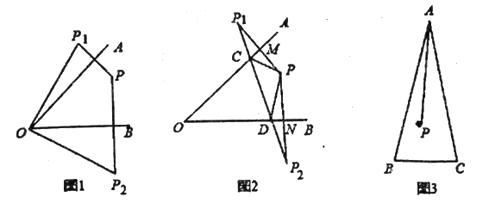
、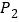 .
.
①如图1,若
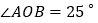 ,请直接写出
,请直接写出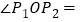 ______;
______;②如图2,连接
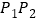 分别交
分别交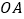 、
、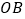 于
于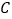 、
、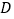 ,若
,若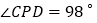 ,求
,求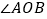 的度数;
的度数;③在②的条件下,若
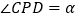 度(
度(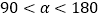 ),请直接写出
),请直接写出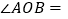 ______度(用含
______度(用含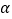 的代数式表示).
的代数式表示).(2)(拓展延伸)利用“有一个角是
 的等腰三角形是等边三角形”这个结论,解答问题:如图3,在
的等腰三角形是等边三角形”这个结论,解答问题:如图3,在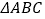 中,
中,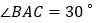 ,点
,点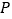 是
是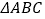 内部一定点,
内部一定点,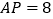 ,点
,点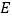 、
、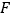 分别在边
分别在边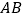 、
、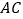 上,请你在图3中画出使
上,请你在图3中画出使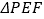 周长最小的点
周长最小的点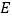 、
、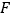 的位置(不写画法),并直接写出
的位置(不写画法),并直接写出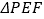 周长的最小值.
周长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=kx+b与反比例函数
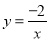 的图象交于A(﹣1,m)、B(n,﹣1)两点.
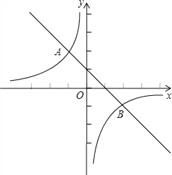
的图象交于A(﹣1,m)、B(n,﹣1)两点.(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乳品公司向某地运输一批牛奶,由铁路运输每千克需运费0.60元,由公路运输,每千克需运费0.30元,另需补助600元
(1)设该公司运输的这批牛奶为x千克,选择铁路运输时,所需运费为y1元,选择公路运输时,所需运费为y2元,请分别写出y1、y2与x之间的关系式;
(2)若公司只支出运费1500元,则选用哪种运输方式运送的牛奶多?若公司运送1500千克牛奶,则选用哪种运输方式所需费用较少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l过正方形ABCD的顶点B,点A、C至直线l的距离分别为2和3,则此正方形的面积为( )
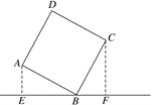
A. 5 B. 6 C. 9 D. 13
-
科目: 来源: 题型:
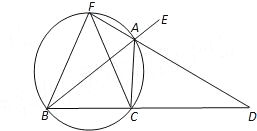
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点分别为(4,0),(4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP,垂足为P,则点P的坐标为_____.
相关试题

