【题目】如图,在□ABCD中,点E、F是对角线BD上的两点,且BE=DF.

(1)求证:四边形AECF是平行四边形.
(2)如果四边形ABCD是菱形,求证:四边形AECF也是菱形.
(3)如果四边形ABCD是矩形,请判断四边形AECF的形状,不必写出证明过程.
参考答案:
【答案】(1)见详解;(2)见详解;(3)四边形AECF是平行四边形.
【解析】
(1)根据两条对角线相互平分的四边形是平行四边形即可证明四边形AECF是平行四边形;(2)根据对角线互相垂直的四边形是菱形即可证明;
(3)因为矩形的对角线相等,根据对角线互相平分的四边形可判定AECF的形状.
证明:(1)如图,连AC,设AC、BD相交于点O,
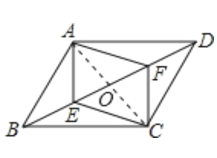 ,
,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=FD,
∴OB-BE=OD-DF,即OE=OF,
∴四边形AECF是平行四边形;
(2)∵四边形ABCD是菱形,
∴AC⊥BD,即AC⊥EF;
由(1)得:四边形AECF是平行四边形,
∴四边形AECF是菱形;
(3)∵四边形ABCD是矩形,
∴OA=OC,OB=OD,
∵BE=FD,
∴OB-BE=OD-DF,即OE=OF,
∴四边形AECF是平四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,A,B,C三点分别为(4,0),(4,4),(0,4),点P在x轴上,点D在直线AB上,若DA=1,CP⊥DP,垂足为P,则点P的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 O
O 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线 和
和 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2( ,
,  ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
-
科目: 来源: 题型:
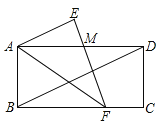
查看答案和解析>>【题目】如图,把一个长方形纸条ABCD沿AF折叠,点B落在点E处.已知∠ADB=24°,AE∥BD,则∠AFE的度数是__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长青化工厂与A、B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8000元的产品运到B地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.

求:(1)该工厂从A地购买了多少吨原料?制成运往B地的产品多少吨?
(2)这批产品的销售款比原料费与运输费的和多多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】从三角形(不是等腰三角形)一个顶点引出一条射线于对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC=
 ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.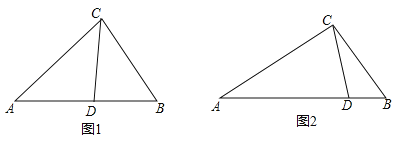
相关试题

