【题目】某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
参考答案:
【答案】(1) y=﹣2x2+120x﹣1600,20≤x≤40;(2) 30元/千克, 200元;(3)25.
【解析】
试题分析:(1)根据销售利润y=(每千克销售价﹣每千克成本价)×销售量w,即可列出y与x之间的函数关系式;
(2)先利用配方法将(1)的函数关系式变形,再利用二次函数的性质即可求解;
(3)先把y=150代入(1)的函数关系式中,解一元二次方程求出x,再根据x的取值范围即可确定x的值.
试题解析:(1)y=w(x﹣20)
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
则y=﹣2x2+120x﹣1600.
由题意,有![]() ,
,
解得20≤x≤40.
故y与x的函数关系式为:y=﹣2x2+120x﹣1600,自变量x的取值范围是20≤x≤40;
(2)∵y=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∴当x=30时,y有最大值200.
故当销售价定为30元/千克时,每天可获最大销售利润200元;
(3)当y=150时,可得方程﹣2x2+120x﹣1600=150,
整理,得x2﹣60x+875=0,
解得x1=25,x2=35.
∵物价部门规定这种产品的销售价不得高于28元/千克,∴x2=35不合题意,应舍去.
故当销售价定为25元/千克时,该农户每天可获得销售利润150元.
考点: 1.二次函数的应用;2.一元二次方程的应用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,命题p:“B≠60°“,命题q:“△ABC的三个内角A,B,C不成等差数列“,那么p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件 -
科目: 来源: 题型:
查看答案和解析>>【题目】将代数式4a2b+3ab2﹣2b2+a3按a的升幂排列的是( )
A.﹣2b3+3ab2+4a2b+a3
B.a3+4a2b+3ab2﹣2b3
C.4a2b+3ab2﹣2b3+a3
D.4a2b+3ab2+a3﹣2b3 -
科目: 来源: 题型:
查看答案和解析>>【题目】有七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙、丙两位同学要站在一起,则不同的站法有( )
A.240种
B.192种
C.96种
D.48种 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:
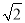 ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)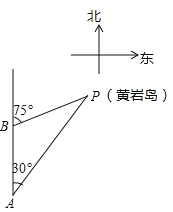
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在抄分解因式的题目时,不小心漏抄了x的指数,他只知道该数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子是x□﹣4y2(“□”表示漏抄的指数),则这个指数可能的结果共有( )
A. 2种 B. 3种 C. 4种 D. 5种
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将ABCD的边BA延长到点E,使AE=AB,连接EC,交AD于点F,连接AC、ED.
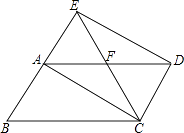
(1)求证:四边形ACDE是平行四边形;
(2)若∠AFC=2∠B,求证:四边形ACDE是矩形.
相关试题

