【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
参考答案:
【答案】(1)直线经过A点;(2)B(1,1)或B(3,1);(3)①正确,②正确.
【解析】
(1)将抛物线解析式整理成顶点式形式,然后写出顶点A的坐标, 将点A的坐标代入直线的解析式判断即可;
(2)![]() △OAB面积为1时,根据三角形的面积公式,求出点B的纵坐标,代入抛物线的解析式即可求出点B的横坐标,即可求解.
△OAB面积为1时,根据三角形的面积公式,求出点B的纵坐标,代入抛物线的解析式即可求出点B的横坐标,即可求解.
(3)①点M(t,0),则点P(t,t2﹣4t+4),点Q(t,kt﹣2k),若k>0:当0≤t≤2时,P在Q点上方时,![]() 整理得t2﹣(4+k)t+(1+2k)=0,求出△=b2﹣4ac=(4+k)2﹣4(1+2k)=k2+12>0,此方程有解,则存在实数t(0≤t≤2)使得PQ=3.
整理得t2﹣(4+k)t+(1+2k)=0,求出△=b2﹣4ac=(4+k)2﹣4(1+2k)=k2+12>0,此方程有解,则存在实数t(0≤t≤2)使得PQ=3.
②分当 P在Q点下方,当P在Q点上方时,两种情况进行分类讨论.
(1)![]()
顶点A(2,0)
当x=2时,由2k-2k=0,
∴直线经过A点.
(2)![]()
△OAB面积为1时,
![]()
![]()
令![]()
解得:![]()
即点B的坐标为:B(1,1)或B(3,1),
(3)∵点M(t,0),
∴点P(t,t2﹣4t+4),点Q(t,kt﹣2k),
①若k>0:当0≤t≤2时,P在Q点上方时,∵PQ=3
∴t2﹣(4+k)t+(4+2k)=3
整理得t2﹣(4+k)t+(1+2k)=0
∵△=b2﹣4ac=(4+k)2﹣4(1+2k)=k2+12>0,此方程有解
∴①正确.
②若k<0:
1)当 P在Q点下方,
∴t2﹣(4+k)t+(4+2k)=﹣3
∴t2﹣(4+k)t+7+2k=0
∵△=b2﹣4ac=(4+k)2﹣4(7+2k)=k2﹣12
∴当存在PQ=3时,k2﹣12≥0
∴k≤![]() 或k≥
或k≥![]() (舍去)
(舍去)
∴当﹣2<k<﹣0.5时,不存在满足条件的t,
2)当P在Q点上方时,
∴t2﹣(4+k)t+(4+2k)=3
∵△=k2+12>0,此方程有解
又∵![]() ∴有一正一负两根
∴有一正一负两根
![]()
∴正根>2
∴在[0,2]上不存在满足条件的t,
∴②正确-
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图
 ,
,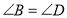 ,那么
,那么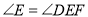 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.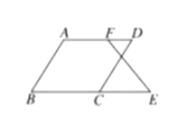
解:成立,理由如下:
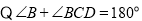 (已知)
(已知) ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)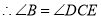 (② )
(② )又
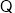
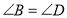 (已知),
(已知),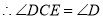 (等量代换)
(等量代换)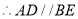 (③ )
(③ )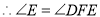 (④ ).
(④ ). -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
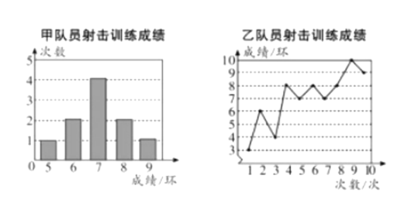
根据以上信息,整理分析数据如下:
平均数(环)
中位数(环)
众数(环)
方差
甲
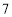
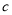
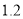
乙
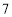
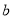
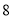
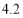
(1)表格中
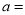 ,
,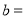 ,
,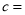 ;
;(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击
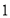 次,命中
次,命中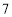 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
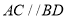 ,连接
,连接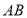 ,
,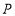 为一动点.
为一动点.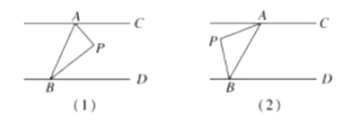
(1)当动点
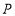 落在如图
落在如图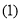 所示的位置时,连接
所示的位置时,连接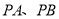 ,求证:
,求证: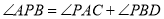 ;
;(2)当动点
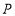 落在如图
落在如图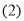 所示的位置时,连接
所示的位置时,连接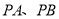 ,则
,则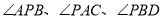 之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
之间的关系如何,你得出的结论是 .(只写结果,不用写证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坡顶
 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔 ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底 处测得该塔的塔顶
处测得该塔的塔顶 的仰角为
的仰角为 ,然后他们沿着坡度为
,然后他们沿着坡度为 的斜坡
的斜坡 攀行了
攀行了 米,在坡顶
米,在坡顶 处又测得该塔的塔顶
处又测得该塔的塔顶 的仰角为
的仰角为 .求古塔
.求古塔 的高度.(结果精确到
的高度.(结果精确到 米,参考数据:
米,参考数据:  ,
,  ,
,  )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(120>x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,月销售额为14000元,此月共盈利多少元.
相关试题

