【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
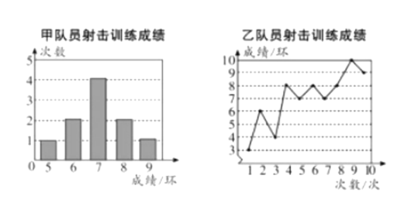
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
参考答案:
【答案】(1)7;7.5;7(2)乙,理由见解析;(3)变小.
【解析】
(1)利用平均数的计算公式直接计算平均分即可;将乙的成绩从小到大重新排列,用中位数的定义直接写出中位数即可;根据乙的平均数利用方差的公式计算即可;
(2)结合平均数和中位数、众数、方差三方面的特点进行分析;
(3)根据方差公式即可求解判断.
(1)甲的平均成绩a=![]() =7(环),
=7(环),
甲的成绩的众数c=7(环),
∵乙射击的成绩从小到大重新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b=![]() =7.5(环),
=7.5(环),
故答案为7;7.5;7
(2)从平均成绩看甲、乙二人的成绩相等均为7环,
从中位数看甲射中7环以上的次数小于乙,
从众数看甲射中7环的次数最多而乙射中8环的次数最多,
从方差看甲的成绩比乙的成绩稳定;
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大;
(3)乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差为:
环,那么乙的射击成绩的方差为:
![]() ×[(37)2+(47)2+(67)2+3×(77)2+3×(87)2+(97)2+(107)2]
×[(37)2+(47)2+(67)2+3×(77)2+3×(87)2+(97)2+(107)2]
=![]() ×(16+9+1+3+4+9)
×(16+9+1+3+4+9)
≈3.8.
故方差变小
故答案为:变小.
-
科目: 来源: 题型:
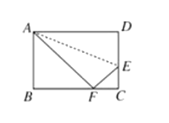
查看答案和解析>>【题目】如图,折叠长方形
 ,使顶点
,使顶点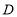 与
与 边上的点
边上的点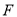 重合,已知长方形
重合,已知长方形 的长度为
的长度为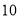 ,宽为
,宽为 ,则
,则 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图
 ,
,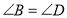 ,那么
,那么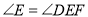 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.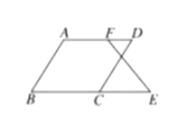
解:成立,理由如下:
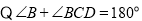 (已知)
(已知) ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)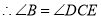 (② )
(② )又
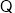
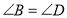 (已知),
(已知),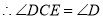 (等量代换)
(等量代换)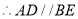 (③ )
(③ )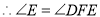 (④ ).
(④ ). -
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y1=x2﹣4x+4的顶点为A,直线y2=kx﹣2k(k≠0),
(1)试说明直线是否经过抛物线顶点A;
(2)若直线y2交抛物线于点B,且△OAB面积为1时,求B点坐标;
(3)过x轴上的一点M(t,0)(0≤t≤2),作x轴的垂线,分别交y1,y2的图象于点P,Q,判断下列说法是否正确,并说明理由:
①当k>0时,存在实数t(0≤t≤2)使得PQ=3.
②当﹣2<k<﹣0.5时,不存在满足条件的t(0≤t≤2)使得PQ=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
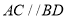 ,连接
,连接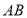 ,
,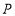 为一动点.
为一动点.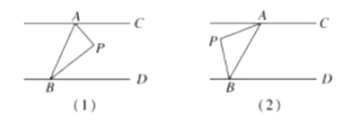
(1)当动点
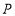 落在如图
落在如图 所示的位置时,连接
所示的位置时,连接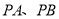 ,求证:
,求证: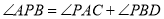 ;
;(2)当动点
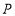 落在如图
落在如图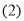 所示的位置时,连接
所示的位置时,连接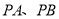 ,则
,则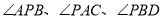 之间的关系如何,你得出的结论是 .(只写结果,不用写证明)
之间的关系如何,你得出的结论是 .(只写结果,不用写证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在坡顶
 处的同一水平面上有一座古塔
处的同一水平面上有一座古塔 ,数学兴趣小组的同学在斜坡底
,数学兴趣小组的同学在斜坡底 处测得该塔的塔顶
处测得该塔的塔顶 的仰角为
的仰角为 ,然后他们沿着坡度为
,然后他们沿着坡度为 的斜坡
的斜坡 攀行了
攀行了 米,在坡顶
米,在坡顶 处又测得该塔的塔顶
处又测得该塔的塔顶 的仰角为
的仰角为 .求古塔
.求古塔 的高度.(结果精确到
的高度.(结果精确到 米,参考数据:
米,参考数据:  ,
,  ,
,  )
)
相关试题

