【题目】(12分)如图1,抛物线![]() 与
与![]() 轴交于A(1,0),B(-3,0),与
轴交于A(1,0),B(-3,0),与![]() 轴交于C(0,3),顶点是G.
轴交于C(0,3),顶点是G.
(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线![]() 向下平移
向下平移![]() 个单位,平移后的顶点式
个单位,平移后的顶点式![]() ,与
,与![]() 轴的交点是
轴的交点是![]() .若△
.若△![]() 是锐角三角形,求
是锐角三角形,求![]() 的取值范围.
的取值范围.


参考答案:
【答案】(1)![]() ,G(-1,4);(2)
,G(-1,4);(2)![]() (
(![]() ),当
),当![]() 时,
时, ![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)利用二次函数的双根式得抛物线的解析式,并根据顶点式求顶点.
(2)先求出直线 BG的解析式,D在直线上,所以可表示出D的坐标,利用梯形面积公式,用x表示四边形的面积S,得二次函数,配方求最值.
(3)找临界条件,恰好△![]() 是直角三角形,可求出k的值.
是直角三角形,可求出k的值.
试题解析:
解:(1) ∵与![]() 轴的交点为A(1,0),B(-3,0),
轴的交点为A(1,0),B(-3,0),
∴设二次函数为![]() ,
,
把C(0, 3)代入![]() ,
,
∴![]() ∴
∴![]() ,
,
∴ G(-1,4).
(2)设直线BG解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (
(![]() ),
),
当![]() 时,
时, ![]() .
.
(3)设平移后的抛物线为![]() ,且此时△A’B’G’为直角三角形
,且此时△A’B’G’为直角三角形
∵![]() 又∵△A’B’G’为直角三角形,
又∵△A’B’G’为直角三角形,
∴![]() ,
,
将点![]() 代入得:
代入得: ![]() ,
,
∴![]() ,
, ![]() (舍) ,
(舍) ,
∴![]() ,
,
由![]() 得到
得到![]() 向下平移3个单位,
向下平移3个单位,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(-1,3),B(-1,-1),下列四个点中,在线段AB的垂直平分线上的是( )
A. (0,2) B. (-3,1) C. (1,2) D. (1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)已知AB是⊙O的直径,C是圆周上的动点,P是优弧
 中点.
中点.(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣5+|﹣3|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)已知二次函数
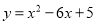 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】芝麻作为食品和药物,均广泛使用,经测算,一粒芝麻重量约有0.00 000 201kg,用科学记数法表示10粒芝麻的重量为( )
A. 2.01×10﹣6kg B. 2.01×10﹣5kg C. 20.1×10﹣7kg D. 20.1×10﹣6kg
-
科目: 来源: 题型:
查看答案和解析>>【题目】样本数据3,2,4,a,8的平均数是4,则这组数据的众数是( )
A.2
B.3
C.4
D.8
相关试题

