【题目】(8分)已知AB是⊙O的直径,C是圆周上的动点,P是优弧![]() 中点.
中点.
(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接AC,延长PO交AC于H,根据垂径定理OH ![]() ,∠ACB=90°,所以OP∥BC得证.
,∠ACB=90°,所以OP∥BC得证.
(2) 设∠OPC=x,利用圆中两条半径特有的等腰三角形,同弧所对圆周角是圆心角的一半,用x表示△COD内角和,求出x.
(1)证明:连接AC,延长PO交AC于H,如图1,

∵P是优弧![]() 的中点, ∴PH⊥AC,
的中点, ∴PH⊥AC,
∵AB是⊙O的直径, ∴∠ACB=90°,
∴BC⊥AC, ∴OP∥BC;
(2)连接AC,延长PO交AC于H,如图2,
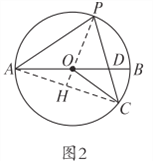
∵P是优弧![]() 的中点, ∴PA=PC, ∴∠PAC=∠PCA,
的中点, ∴PA=PC, ∴∠PAC=∠PCA,
∵OA=OC, ∴∠OAC=∠OCA, ∴∠PAO=PCO,
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x, ∴∠PDO=2x,
∴∠ODC=∠POD+∠OPC=3x,
∵CD=CO, ∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=![]() ,即∠PAO=
,即∠PAO=![]() ,∴∠A的度数为
,∴∠A的度数为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)在湖州创建国家卫生文明城市的过程中,张辉和夏明积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①清理类岗位:清理花坛卫生死角;清理楼道杂物(分别用
 表示).
表示).②宣传类岗位:垃圾分类知识宣传;交通安全知识宣传(分别用
 表示).
表示).(1)张辉同学从四个岗位中随机选取一个报名,恰好选择清理类岗位概率为是 ;
(2)若张辉和夏明各随机从四个岗位中选一个报名,请你利用树状图或列表法求出他们恰好都选择同一个岗位的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知A(-1,3),B(-1,-1),下列四个点中,在线段AB的垂直平分线上的是( )
A. (0,2) B. (-3,1) C. (1,2) D. (1,0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣5+|﹣3|= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图1,抛物线
 与
与 轴交于A(1,0),B(-3,0),与
轴交于A(1,0),B(-3,0),与 轴交于C(0,3),顶点是G.
轴交于C(0,3),顶点是G.(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线
 向下平移
向下平移 个单位,平移后的顶点式
个单位,平移后的顶点式 ,与
,与 轴的交点是
轴的交点是 .若△
.若△ 是锐角三角形,求
是锐角三角形,求 的取值范围.
的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)已知二次函数
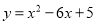 的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.
的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D.(1)求以A,B,C,D为顶点的四边形的面积;
(2)在抛物线上是否存在点P,使得△ABP的面积是△ABC的面积的2倍?若存在,求出点P的坐标;若不存在,请说明理由.
相关试题

