【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.已知∠ACB=30°,AB=1,
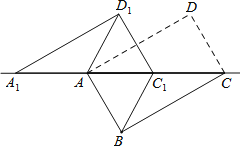
(1)求证:△A1AD1≌△CC1B;
(2)当CC1=1时,求证:四边形ABC1D1是菱形。
参考答案:
【答案】证明见解析
【解析】试题分析:(1)由矩形的性质及平移的性质易得∠A1=∠DAC,A1D1=AD,AA1=CC1,即可得到结论;
(2)由所给条件可证明△AC1B是等边三角形,即可得到ABC1D1是菱形.
试题解析:解:(1)∵四边形ABCD为矩形,
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠AA1 D1=∠DAC,A1D1=AD,AA1=CC1,
∴∠AA1 D1=∠ACB, BC= A1D1
在△A1AD1与△CC1B中,
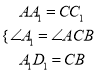 ,
,
∴△A1AD1≌△CC1B;
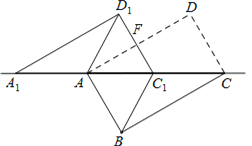
(2)证明∵∠ACB=30°,∴∠CAB=60°.
∵AB=1,∴AC=2.
∵CC1=1,∴AC1=1,∴△AC1B是等边三角形,.
∵AB=CD,CD=C1D1,∴AB= C1D1,∴四边形ABC1D1是平行四边形.
又AB=BC1,∴四边形ABC1D1是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选择适当方法解下列方程:
(1)
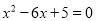
(2)
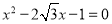
(3)
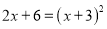
(4) -
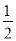 x2-3x+6=0;
x2-3x+6=0; -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为加强学生的安全意识,每周通过安全教育APP软件,向家长和学生推送安全教育作业.在最近一期的防溺水安全知识竞赛中,从中抽取了部分学生成绩进行统计.绘制了图中两幅不完整的统计图.请回答如下问题:

(1)m= ,a= ;
(2)补全频数直方图;
(3)该校共有1600名学生.若认定成绩在60分及以下(含60分)的学生安全意识不强,有待进一步加强安全教育,请估计该校安全意识不强的学生约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四张质地相同的卡片如图所示.将卡片洗匀后,背面朝上放置在桌面上.

(1)求随机抽取一张卡片,恰好得到数字2的概率;
(2)小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树形图法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对于直线MN同侧的两个点A,B,若直线MN上的点P满足∠APM=∠BPN,则称点P为A,B在直线MN上的反射点.已知如图2,MN∥HG,AP∥BQ,点P为A,B在直线MN上的反射点,判断点B是否为P,Q在直线HG上的反射点,如果是请证明,如果不是,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在△ABC中,DE∥BC分别交AB于D,交AC于E.已知CD⊥BE,CD=3,BE=4,求BC+DE的值.
小明发现,过点E作EF∥DC,交BC延长线于点F,构造△BEF,经过推理和计算能够使问题得到解决(如图2).

(1)请按照上述思路完成小明遇到的这个问题
(2)参考小明思考问题的方法,解决问题:
如图3,已知ABCD和矩形ABEF,AC与DF交于点G,AC=BF=DF,求∠DGC的度数.
相关试题

