搜索
【题目】如图，点C在线段AB上，线段AC=8cm，BC=4cm，点M、N分别是AC、BC的中点， 求：
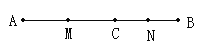
（1） 线段MN的长度．
（2） 根据（1）的计算过程和结果，设AC+BC=
，其它条件不变，你能猜测出MN的长度吗？请证明你的猜测．
参考答案：
【答案】(1)6cm；（2）
；证明见解析
【解析】
（1）根据点M、N分别是AC、BC的中点，先求出MC、CN的长度，再利用MN=CM+CN即可求出MN的长度即可，
（2）根据点M、N分别是AC、BC的中点，可知CM=
AC，CN=BC，再利用MN=CM+CN即可求出MN的长度．
解：（1）∵点M、N分别是AC、BC的中点，
∴CM=AC=4cm，
CN=BC=2cm，
∴MN=CM+CN=4+2=6cm，
（2）猜测MN=a，
∵点M、N分别是AC、BC的中点，
∴CM=AC，
CN=BC，
∴MN=CM+CN=（AC+BC）=a．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量y（单位:个）与销售单价x（单位:元）有如下关系：y=－x+60（30≤x≤60）．
设这种双肩包每天的销售利润为w元．
（1）求w与x之间的函数解析式；
（2）这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种双肩包的销售单价不高于48元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
，
两点在数轴上，点在原点
的左边，表示的数为－15，点在原点的右边，且
．点
以每秒3个单位长度的速度从点出发向右运动．点
以每秒2个单位长度的速度从点出发向右运动（点，点同时出发）．
（1）数轴上点
对应的数是______，点到点的距离是______；（2）经过几秒，原点
是线段
的中点？（3）经过几秒，点
，分别到点的距离相等？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠ACB=90°，在以AB的中点O为坐标原点，AB所在直线为x轴建立的平面直角坐标系中，将△ABC绕点B顺时针旋转，使点A旋转至y轴的正半轴上的A′处，若AO=OB=2，则阴影部分面积为（ ）
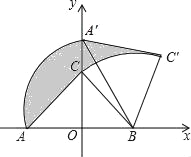
A.
π B. π﹣1 C. 
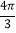+1 D. -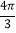
科目： 来源： 题型：
查看答案和解析>>【题目】为了提高学生书写汉字的能力，增强保护汉子的意识，某校举办了首届“汉字听写大赛”，学生经选拔后进入决赛，测试同时听写100个汉字，每正确听写出一个汉字得1分，本次决赛，学生成绩为
（分），且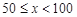
，将其按分数段分为五组，绘制出以下不完整表格：组别
成绩
（分）频数（人数）
频率
一
2
0.04
二
10
0.2
三
14
b
四
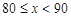
a
0.32
五
8
0.16
请根据表格提供的信息，解答以下问题：
（1）本次决赛共有 名学生参加；
（2）直接写出表中a= ,b= ;
（3）请补全下面相应的频数分布直方图；
（4）若决赛成绩不低于80分为优秀，则本次大赛的优秀率为 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知有理数a，b在数轴上的位置如图所示．
（1）在数轴上标出﹣a，﹣b的位置，并比较a，b，﹣a，﹣b的大小：
（2）化简|a+b|+|a﹣b|．
-
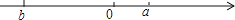
科目： 来源： 题型：
查看答案和解析>>【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4，把y=t（x2﹣3x+2）+（1﹣t）（﹣2x+4）称为这两个函数的“再生二次函数”，其中t是不为零的实数，其图象记作抛物线L．现有点A（2，0）和抛物线L上的点B（﹣1，n），请完成下列任务：
【尝试】
（1）当t=2时，抛物线y=t（x2﹣3x+2）+（1﹣t）（﹣2x+4）的顶点坐标为 ；
（2）判断点A是否在抛物线L上；
（3）求n的值；
【发现】
通过（2）和（3）的演算可知，对于t取任何不为零的实数，抛物线L总过定点，坐标为 ．
【应用】
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗？如果是，求出t的值；如果不是，说明理由．
相关试题
