【题目】如图,已知FG⊥AB,CD⊥AB,垂足分别为G,D,∠1=∠2,
求证:∠CED+∠ACB=180°,
请你将小明的证明过程补充完整.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°( ).
∴GF∥CD( )
∵GF∥CD(已证)
∴∠2=∠BCD( )
又∵∠1=∠2(已知)
∴∠1=∠BCD( )
∴ ( )
∴∠CED+∠ACB=180°( )

参考答案:
【答案】见解析.
【解析】
根据同位角相等两直线平行可得GF∥CD,然后根据两直线平行同位角相等得出∠2=∠BCD,根据已知进一步得出∠1=∠BCD,即可证得DE∥BC,得出∠CED+∠ACB=180°.
证明:∵FG⊥AB,CD⊥AB,垂足分别为G,D(已知)
∴∠FGB=∠CDB=90°(垂直定义).
∴GF∥CD(同位角相等,两直线平行),
∵GF∥CD(已证),
∴∠2=∠BCD(两直线平行,同位角相等),
又∵∠1=∠2(已知),
∴∠1=∠BCD(等量代换),
∴DE∥BC(内错角相等,两直线平行)
∴∠CED+∠ACB=180°(两直线平行,同旁内角互补),
故答案为:垂直定义;同位角相等,两直线平行;两直线平行,同位角相等;等量代换;DE∥BC;内错角相等,两直线平行;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F.

(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,将△ABC在平面内绕点A逆时针旋转50角后得到△AB′C′的位置,若此时恰有CC′∥AB,则∠CAB′的度数为( )

A.15°
B.40°
C.50°
D.65° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
(1)画出△ABC中BC边上的高AH和BC边上的中线AD.
(2)画出将△ABC向右平移5格又向上平移3格后的△A′B′C′.
(3)△ABC的面积为 .
(4)若连接AA′,CC′,则这两条线段之间的关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
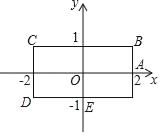
A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分的面积为(结果保留π)( )

A.
B.
C.
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示,已知,BC∥OA,∠B=∠A=100°,试解答下列问题:
(1)试说明:OB∥AC;

(2)如图②,若点E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.试求∠EOC的度数;

(3)在(2)小题的条件下,若左右平行移动AC,如图③,那么∠OCB:∠OFB的比值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

(4)在(3)小题的条件下,当∠OEB=∠OCA时,试求∠OCA的度数.
相关试题

