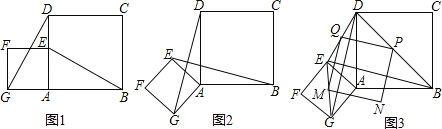
【题目】如图1所示,四边形AEFG与四边形ABCD是正方形,其中G、A、B三点在同一直线上.连接DG、BE.完成下面问题:
(1)求证:BE=DG;
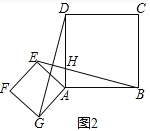
(2)如图2,将正方形AEFG绕点A逆时针转过一定角度时,小明发现:BE=DG且BE⊥DG,请你帮助小明证明这两个结论;
(3)如图3,小明还发现:在旋转过程中,分别连接EG、GB、BD、DE的中点,得到的四边形MNPQ是正方形.若AB=a,AE=b其中a>b,你能帮小明求出正方形MNPQ的面积的范围吗?写出过程.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() (a﹣b)2≤正方形MNPQ的面积≤
(a﹣b)2≤正方形MNPQ的面积≤![]() (a+b)2.
(a+b)2.
【解析】
试题分析:(1)根据正方形的性质得到AD=AB,AE=AG,∠DAG=∠BAE=90°,证明△DAG≌△BAE,根据全等三角形的性质证明结论;
(2)根据全等三角形的性质和互余的概念以及垂直的定义证明即可;
(3)根据三角形中位线定理得到MN=![]() BE,根据旋转的性质和正方形的面积公式计算即可.
BE,根据旋转的性质和正方形的面积公式计算即可.
(1)证明:∵四边形AEFG与四边形ABCD是正方形,
∴AD=AB,AE=AG,∠DAG=∠BAE=90°,
在△DAG和△BAE中,
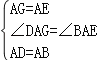 ,
,
∴△DAG≌△BAE,
∴BE=DG;
(2)证明:如图2,∵∠EAG=∠BAD=90°,
∴∠DAG=∠BAE,
在△DAG和△BAE中,
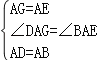 ,
,
∴△DAG≌△BAE,
∴BE=DG,∠ADG=∠ABE,
∵∠ABE+∠AHB=90°,∠AHB=∠DHE,
∴∠ADG+∠DHE=90°,
∴BE⊥DG,
∴BE=DG且BE⊥DG;
(3)解:∵M、N分别是EG、GB的中点,
∴MN=![]() BE,
BE,
∴当BE最小时,正方形MNPQ是面积最小,BE最大时,正方形MNPQ是面积最大,
由题意可知,当点E旋转到线段AB上时,BE最小为a﹣b,
当点E旋转到线段AB的延长线上时,BE最答为a+b,
∴![]() (a﹣b)2≤正方形MNPQ的面积≤
(a﹣b)2≤正方形MNPQ的面积≤![]() (a+b)2.
(a+b)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中, 若∠A :∠B :∠C = 1 : 2 : 3 , 则△ABC 是( )
A. 锐角三角形. B. 直角三角形 C. 钝角三角形 D. 等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )
A.0.25×10-5 B.0.25×10-6 C.2.5×10-5 D.2.5×10-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2+px+q=0有两个根是x1,x2,那么x1+x2=﹣p,x1x2=q,请根据以上结论,解决下列问题:
(1)已知关于x的方程x2+2x﹣5=0,求(x1+2)(x2+2)和(
 +
+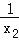 )的值;
)的值;(2)已知a,b满足a2﹣15a﹣5=0,b2﹣15b﹣5=0,求
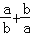 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的布袋里装有3个小球,其中2个红球,1个白球,它们除颜色外其余都相同.
(1)求摸出1个小球是白球的概率;
(2)摸出1个小球,记下颜色后放回,并搅均,再摸出1个小球.求两次摸出的小球恰好颜色不同的概率.(要求画树状图或列表)
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[1,m-3]的一次函数是正比例函数,则关于x的方程mx-6=0的解为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个人患了流感,经过两轮传染后共有121人患了流感;因此一个人传染了 个人,三轮共有 人患了流感.(期间无人治愈)
相关试题

