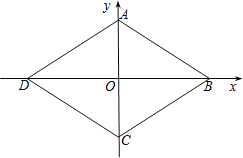
【题目】如图，在平面直角坐标系中，菱形ABCD的四个顶点均在坐标轴上，A（0，2），∠ABC=60°．把一条长为2013个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在菱形ABCD的边上，则细线另一端所在位置的点的坐标是（ ）

A．（，） B．（，﹣） C．（﹣，） D．（﹣，）

参考答案：

【答案】C

【解析】

试题分析：根据A的坐标和∠ABC=60°，求出菱形的边长和周长，然后求出另一端是绕第几圈后的第几个单位长度，从而确定答案．

解：∵A（0，2），

∴AC=4，

∵∠ABC=60°，

∴AB=BC=CD=DA=4，菱形的周长为16，

即绕菱形ABCD一周的细线长度为16，

2013÷16=125…13，

则细线另一端在绕四边形第125圈的第13个单位长度的位置，

即此时细线另一端在AD边上，且距离D点为1个单位长度，距离A点3个单位长度，

设AD所在的直线为y=kx+b，

∵∠ABC=60°，A（0，2），

∴D（﹣2，0），

把点的坐标代入求解析式得：y=﹣x+2，

即CD所在直线为y=﹣x+2，

把选项中各点代入，满足题意的为（﹣，）．

故选C．

关闭