Question

【题目】如图，在矩形纸片ABCD中，AB=4，AD=12，将矩形纸片折叠，使点C落在AD边上的点M处，折痕为PE，此时PD=3．

（1）求MP的值
（2）在AB边上有一个动点F，且不与点A，B重合．当AF等于多少时，△MEF的周长最小？
（3）若点G，Q是AB边上的两个动点，且不与点A，B重合，GQ=2．当四边形MEQG的周长最小时，求最小周长值．（计算结果保留根号）

Answer 1

【答案】
（1）

解：∵四边形ABCD为矩形，

∴CD=AB=4，∠D=90°，

∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，

∴PD=PH=3，CD=MH=4，∠H=∠D=90°，

∴MP==5；

（2）

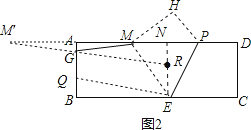
解：如图1，作点M关于AB的对称点M′，连接M′E交AB于点F，则点F即为所求，过点E作EN⊥AD，垂足为N，

∵AM=AD﹣MP﹣PD=12﹣5﹣3=4，

∴AM=AM′=4，

∵矩形ABCD折叠，使点C落在AD边上的点M处，折痕为PE，

∴∠CEP=∠MEP，

而∠CEP=∠MPE，

∴∠MEP=∠MPE，

∴ME=MP=5，

在Rt△ENM中，MN===3，

∴NM′=11，

∵AF∥ME，

∴△AFM′∽△NEM′，

∴=，即=，解得AF=，

即AF=时，△MEF的周长最小.

（3）

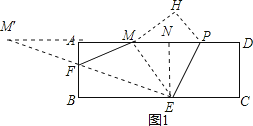
解：如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，

∵ER=GQ，ER∥GQ，

∴四边形ERGQ是平行四边形，

∴QE=GR，

∵GM=GM′，

∴MG+QE=GM′+GR=M′R，此时MG+EQ最小，四边形MEQG的周长最小，

在Rt△M′RN中，NR=4﹣2=2，

M′R==5，

∵ME=5，GQ=2，

∴四边形MEQG的最小周长值是7+5．

【解析】（1）根据折叠的性质和矩形性质以得PD=PH=3，CD=MH=4，∠H=∠D=90°，然后利用勾股定理可计算出MP=5；
（2）如图1，作点M关于AB的对称点M′，连接M′E交AB于点F，利用两点之间线段最短可得点F即为所求，过点E作EN⊥AD，垂足为N，则AM=AD﹣MP﹣PD=4，所以AM=AM′=4，再证明ME=MP=5，接着利用勾股定理计算出MN=3，所以NM′=11，然后证明△AFM′∽△NEM′，则可利用相似比计算出AF；
（3）如图2，由（2）知点M′是点M关于AB的对称点，在EN上截取ER=2，连接M′R交AB于点G，再过点E作EQ∥RG，交AB于点Q，易得QE=GR，而GM=GM′，于是MG+QE=M′R，利用两点之间线段最短可得此时MG+EQ最小，于是四边形MEQG的周长最小，在Rt△M′RN中，利用勾股定理计算出M′R=5 ， 易得四边形MEQG的最小周长值是7+5．
此题考查了几何图形中的折叠问题，涉及勾股定理，三角形相似以及最值问题。