【题目】如图，是由若干个完全相同的小正方体组成的一个几何体．
（1）请画出这个几何体的左视图和俯视图；（用阴影表示）
（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的俯视图和左视图不变，那么最多可以再添加几个小正方体？

参考答案：

【答案】解：（1）画图如下：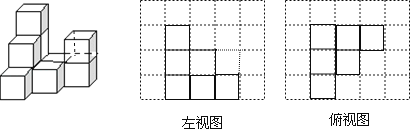

（2）在第二层第二列第二行和第三行各加一个；第三层第二列第三行加一个，第三列第三行加1个，
2+1+1=4（个）．
故最多可再添加4个小正方体．
【解析】（1）由已知条件可知，左视图有3列，每列小正方形数目分别为3，2，1；俯视图有3列，每列小正方数形数目分别为3，2，1，据此可画出图形．
　　　　（2）可在第二层第二列第二行和第三行各加一个；第三层第二列第三行加一个，第三列第三行加1个，相加即可求解．
【考点精析】利用三视图的画法对题目进行判断即可得到答案，需要熟知在画物体的三视图时，对看得见的轮廓线用实线画出，而对看不见的轮廓线要用虚线画出．在三种视图中，主视图反映的是物体的长和高、俯视图反映的是物体的长和宽、左视图反映的是物体的宽和高.因此，在画三视图时，对应部分的长要相等．

关闭