【题目】已知,如图MN∥PQ,点A、B分别在MN、PQ上,∠ABP=80°,射线BC平分∠ABP,且∠CAM=25°,则∠ACB的度数为__________________.

参考答案:
【答案】15°或65°
【解析】
由于MN∥PQ,那么∠ADB=∠CBP,而∠ABP=80°,BC平分∠ABP,易求∠CBP,进而可知∠ADB,结合三角形外角性质分两种情况,当AC在直线MN的上方时和当AC在直线MN的下方时,可求∠ACB.
解:如图,
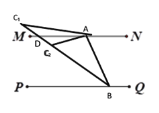
∵MN∥PQ,
∴∠ADB=∠CBP,
∵∠ABP=80°,BC平分∠ABP,
∴∠CBP=![]() ∠ABP=40°,
∠ABP=40°,
∴∠ADB=40°,
当AC在直线MN的上方时,
∵∠ADB=∠CAM+∠C,∠CAM=25°,
∴∠C=∠ADB-∠CAM=40°-25°=15°.
当AC在直线MN的下方时,
∵∠ACB=∠ADB+∠CAM,∠CAM=25°,
∴∠ACB=40°+25°=65°.
故答案是15°或65°.
-
科目: 来源: 题型:
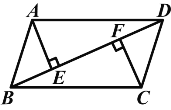
查看答案和解析>>【题目】如图,已知在四边形ABCD中,AE⊥BD于E,CF⊥BD于F,AE=CF,BF=DE.求证:四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=mx+n与双曲线y=
 相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2),B(2,b)两点,与y轴相交于点C. 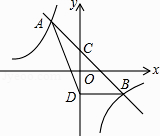
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,0),点B在y轴正半轴上,直线AB与直线l:y=
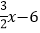 相交于点C,直线l与x轴交于点D,AB=
相交于点C,直线l与x轴交于点D,AB=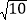 .
.(1)求点D坐标;
(2)求直线AB的函数解析式;
(3)求△ADC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有甲、乙两个不透明的袋子,甲袋内装有标记数字﹣1,2,3的三张卡片,乙袋内装有标记数字2,3,4的三张卡片(卡片除数字不同其余都相同).先从甲袋中随机抽取一张卡片,记录下数字,再从乙袋中随机抽取一张卡片,记录下数字.
(1)利用列表或画树状图的方法(只选其中一种)表示出所抽两张卡片上数字之积所有可能的结果:
(2)求抽出的两张卡片上的数字之积是3的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:
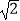 ≈1.414,
≈1.414,  ≈1.732).
≈1.732).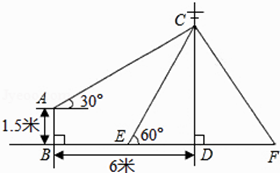
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
相关试题

