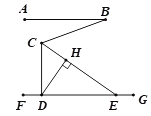
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732).
≈1.732).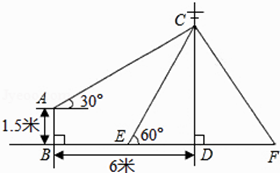
参考答案:
【答案】解:过点A作AH⊥CD,垂足为H,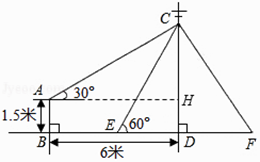
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH= ![]() ,
,
∴CH=AHtan∠CAH,
∴CH=AHtan∠CAH=6tan30°=6× ![]() =2
=2 ![]() ,
,
∵DH=1.5,
∴CD=2 ![]() +1.5,
+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED= ![]() ,
,
∴CE= ![]() =4+
=4+ ![]() ≈5.7(米),
≈5.7(米),
答:拉线CE的长约为5.7米
【解析】过点A作AH⊥CD,垂足为H,在Rt△ACH中求出CH,在Rt△ECD中,再求出EC即可.
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,0),点B在y轴正半轴上,直线AB与直线l:y=
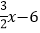 相交于点C,直线l与x轴交于点D,AB=
相交于点C,直线l与x轴交于点D,AB=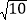 .
.(1)求点D坐标;
(2)求直线AB的函数解析式;
(3)求△ADC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图MN∥PQ,点A、B分别在MN、PQ上,∠ABP=80°,射线BC平分∠ABP,且∠CAM=25°,则∠ACB的度数为__________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有甲、乙两个不透明的袋子,甲袋内装有标记数字﹣1,2,3的三张卡片,乙袋内装有标记数字2,3,4的三张卡片(卡片除数字不同其余都相同).先从甲袋中随机抽取一张卡片,记录下数字,再从乙袋中随机抽取一张卡片,记录下数字.
(1)利用列表或画树状图的方法(只选其中一种)表示出所抽两张卡片上数字之积所有可能的结果:
(2)求抽出的两张卡片上的数字之积是3的倍数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11 815元.已知两种球厂家的批发价和商场的零售价如右表,试解答下列问题:
品名
厂家批发价(元/只)
市场零售价(元/只)
篮球
130
160
排球
100
120
(1)该采购员最多可购进篮球多少只?
(2)若该商场把这100只球全部以零售价售出,为使商场获得的利润不低于2580元,则采购员至少要购篮球多少只,该商场最多可盈利多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥FG,CE平分∠BCD,交FG于点E,过点D作DH⊥CE,垂足为H,若∠ABC=20°,则∠CEG-∠CDH=________度.
相关试题

