【题目】用尺规在一个平行四边形内作菱形![]() ,下列作法中错误的是( )
,下列作法中错误的是( )

A. (A) B. (B) C. (C) D. (D)
参考答案:
【答案】C
【解析】由作图,可以证明A、B、D中四边形ABCD是菱形,C中ABCD是平行四边形,即可得到结论.
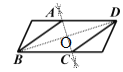
A.∵AC是线段BD的垂直平分线,∴BO=OD,∴∠AOD=∠COB=90°.
∵AD∥BC,∴∠ADB=∠DBC,∴△AOD≌△COB,∴AO=OC,∴四边形ABCD是菱形.故A正确;
B.由作图可知:AD=AB=BC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∵AD=AB,∴四边形ABCD是菱形.故B正确;
C.由作图可知AB、CD是角平分线,可以得到ABCD是平行四边形,不能得到ABCD是菱形.故C错误;
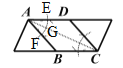
D.如图,∵AE=AF,AG=AG,EG=FG,∴△AEG≌△AFG,∴∠EAG=∠FAG.
∵AD∥BC,∴∠DAC=∠ACB,∴∠FAG=∠ACB,∴AB=BC,同理∠DCA=∠BCA,∴∠BAC=∠DCA,∴AB∥DC.
∵AD∥BC,∴四边形ABCD是平行四边形.
∵AB=BC,∴四边形ABCD是菱形.故D正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读第①小题的计算方法,再计算第②小题.
①–5
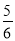 +(–9
+(–9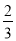 )+17
)+17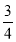 +(–3
+(–3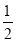 )
)解:原式=[(–5)+(–
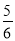 )]+[(–9)+(–
)]+[(–9)+(–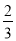 )]+(17+
)]+(17+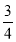 )+[(–3+(–
)+[(–3+(–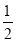 )]
)]=[(–5)+(–9)+(–3)+17]+[(–
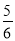 )+(–
)+(–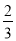 )+(–
)+(–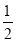 )+
)+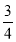 ]
]=0+(–1
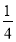 )
)=–1
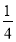 .
.上述这种方法叫做拆项法.灵活运用加法的交换律、结合律可使运算简便.
②仿照上面的方法计算:(﹣2000
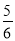 )+(﹣1999
)+(﹣1999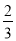 )+4000
)+4000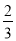 +(﹣1
+(﹣1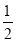 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,
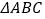 中,
中,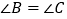 ,
,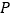 是
是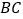 边上一点,作
边上一点,作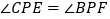 ,分别交边
,分别交边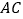 ,
,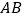 于点
于点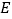 ,
,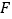 .
.
(1)若
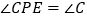 (如图1),求证:
(如图1),求证: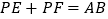 .
.(2)若
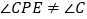 ,过点
,过点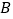 作
作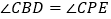 ,交
,交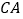 (或
(或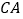 的延长线)于点
的延长线)于点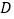 .试猜想:线段
.试猜想:线段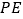 ,
,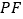 和
和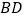 之间的数量关系,并就
之间的数量关系,并就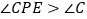 情形(如图2)说明理由.
情形(如图2)说明理由.(3)若点
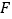 与
与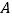 重合(如图3),
重合(如图3),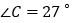 ,且
,且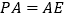 .
.①求
 的度数;
的度数;②设
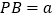 ,
,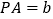 ,
,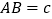 ,试证明:
,试证明: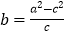 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上点
 表示数
表示数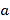 ,点
,点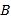 表示数
表示数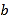 ,点
,点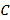 表示数
表示数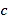 ,
,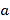 是多项式
是多项式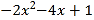 的一次项系数,
的一次项系数,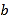 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式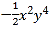 的次数为
的次数为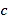 .
.
(1)
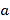 = ,
= ,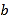 = ,
= ,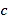 = ;
= ;(2)若将数轴在点
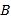 处折叠,则点
处折叠,则点 与点
与点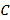 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);(3)点
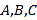 开始在数轴上运动,若点
开始在数轴上运动,若点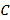 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点 和点
和点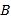 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,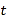 秒钟过后,若点
秒钟过后,若点 与点B之间的距离表示为
与点B之间的距离表示为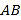 ,点
,点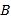 与点
与点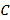 之间的距离表示为
之间的距离表示为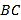 ,则
,则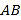 = ,
= , 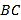 = (用含
= (用含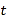 的代数式表示);
的代数式表示);(4)请问:AB+BC的值是否随着时间
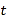 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B,C都在直线l上,点P是线段AC的中点.设
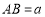 ,
,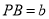 ,则线段BC的长为________(用含a,b的代数式表示)
,则线段BC的长为________(用含a,b的代数式表示) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A,B,C,D,请按要求画出图形.

(1)画直线AB和射线CB;
(2)连结AC,并在直线AB上用尺规作线段AE,使
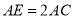 .(要求保留作图痕迹)
.(要求保留作图痕迹)(3)在直线AB上确定一点P,使
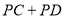 的和最短,并写出画图的依据.
的和最短,并写出画图的依据.
相关试题

