【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是请给出证明,
(3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN.

参考答案:
【答案】(1)(1)CD=BE.理由见解析;(2)△AMN是等边三角形.理由见解析;(3)4:16:7
【解析】试题分析:(1)可以利用SAS判定△ABE≌△ACD,然后根据全等三角形的对应边相等,得到CD=BE.(2)可以证明△AMN是等边三角形,AD=a,则AB=2a,则AB=2a;(3)根据已知条件分别求得△AMN的边长,因为△ADE,△ABC,△AMN为等边三角形,所以面积比等于边长的平方的比,据此解答即可.
(1)CD=BE.理由如下:
∵△ABC和△ADE为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60o.
∵∠BAE =∠BAC-∠EAC =60o-∠EAC,
∠DAC =∠DAE-∠EAC =60o-∠EAC,
∴∠BAE=∠DAC,
∴△ABE ≌ △ACD.
∴CD=BE.
(2)△AMN是等边三角形.理由如下:
∵△ABE ≌ △ACD,
∴∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,
∴BM= ![]() .
.
∵AB=AC,∠ABE=∠ACD,
∴△ABM ≌ △ACN.
∴AM=AN,∠MAB=∠NAC.
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60o.
∴△AMN是等边三角形.
(3) 设AD=a,则AB=2a.
∵AD=AE=DE,AB=AC,
∴CE=DE.
∵△ADE为等边三角形,
∴∠DEC=120 o, ∠ADE=60o,
∴∠EDC=∠ECD=30o,
∴∠ADC=90o.
∴在Rt△ADC中,AD=a,∠ACD=30 o ,
∴ CD= ![]() .
.
∵N为DC中点,
∴![]() ,
,
∴ .
.
∵△ADE,△ABC,△AMN为等边三角形,
∴S△ADE∶S△ABC∶ S△AMN=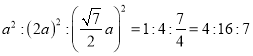
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,一个三角形的三个顶点的坐标,横坐标保持不变,纵坐标增加3个单位,则所得的图形与原图形相比( ).
A. 形状不变,大小扩大了3倍 B. 形状不变,向右平移了3个单位
C. 形状不变,向上平移了3个单位 D. 三角形被纵向拉伸为原来的3倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】电影票上“4排5号”,记作(4,5),则“5排4号”记作______
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x
 .
.(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若
 ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;(3)当
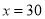 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: ①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ,75);
,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 .
-
科目: 来源: 题型:
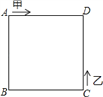
查看答案和解析>>【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣2向上平移4个单位,再向右平移3个单位,得到新的抛物线,那么新的抛物线的表达式是______.
相关试题

