【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )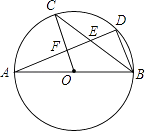
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
参考答案:
【答案】D
【解析】解:①、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,②、∵∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,
∴∠AOC≠∠AEC,③、∵OC∥BD,
∴∠OCB=∠DBC,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OBC=∠DBC,
∴BC平分∠ABD,④、∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BD,
∵OC∥BD,
∴∠AFO=90°,
∵点O为圆心,
∴AF=DF,⑤、由④有,AF=DF,
∵点O为AB中点,
∴OF是△ABD的中位线,
∴BD=2OF,⑥∵△CEF和△BED中,没有相等的边,
∴△CEF与△BED不全等,
故答案为:D
①、根据AB是⊙O的直径得出结论;② 在△AOF和△CFE中,由于∠AOC是⊙O的圆心角,∠AEC是⊙O的圆内部的角,,可知∠AOC≠∠AEC;③、根据同圆的半径相等及平行线的性质可以得出结论;④由垂径定理得出结论;⑤由中位线定理可得出结论;⑥△CEF和△BED中,没有相等的边故得不出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.
a.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是矩形.
b.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是菱形.
c.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )
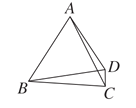
A. 120°B. 135°C. 145°D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中,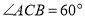 ,
,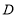 为
为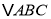 边
边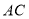 上一点,
上一点,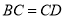 ,
,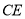 平分
平分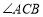 的外角,且
的外角,且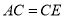 .连接
.连接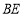 交
交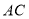 于
于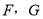 为边
为边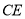 上一点,满足
上一点,满足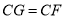 ,连接
,连接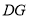 交
交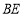 于
于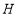 .以下结论:①
.以下结论:①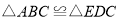 ;②
;②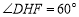 ;③
;③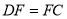 ;④若
;④若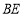 平分
平分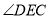 ,则
,则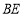 平分
平分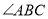 正确的是_____________.
正确的是_____________.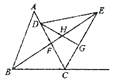
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在⊙O中,AB是弦,半径OC⊥AB,垂足为点D,要使四边形OACB为菱形,还需要添加一个条件,这个条件可以是( )
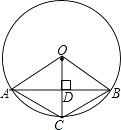
A.AD=BD
B.OD=CD
C.∠CAD=∠CBD
D.∠OCA=∠OCB -
科目: 来源: 题型:
查看答案和解析>>【题目】内部员工互相交换职位是公司培养新人的一种模式,如图1,位于成都的某集团总公司在距离成都
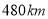 的
的 市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从
市设有一个分公司,现对新入职1年的总公司小颖和分公司小王做职位交换学习,周日早上小颖开车从成都出发,1个小时后,小王开车从 市出发,并以各自的速度匀速行驶,小王到达中途的
市出发,并以各自的速度匀速行驶,小王到达中途的 地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达
地时突然接到分公司紧接通知只好原路原速返回,而小颖还是一直从成都直达 市,结果两人同时到达
市,结果两人同时到达 市.小颖和小王距各自出发地的路程
市.小颖和小王距各自出发地的路程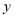 (千米)与小王开车出发所用的时间
(千米)与小王开车出发所用的时间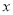 (小时)的关系如图2,结合图象信息解答下列问题:
(小时)的关系如图2,结合图象信息解答下列问题:(1)小颖的速度是____________千米/时,图2中
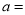 ____________;小王的速度是____________千米/时;
____________;小王的速度是____________千米/时;(2)请写出小王距他的出发地
 市的距离
市的距离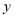 与他出发的时间
与他出发的时间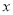 的关系式;
的关系式;(3)直接写出小颖和小王相距100千米时
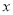 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子中装有四张完全相同的卡片,分别写着2cm,3cm,4cm和5cm,盒子外有两张卡片,分别写着3cm和5cm,现随机从盒中取出一张卡片,与盒子外的两张卡片放在一起,以卡片上的数量分别作为三条线段的长度,那么这三条线段能构成三角形的概率是( )
A.
B.
C.
D.
相关试题

