【题目】如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点.
a.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是矩形.
b.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是菱形.
c.原四边形ABCD的对角线AC、BD满足________时,四边形EFGH是正方形.

参考答案:
【答案】AC⊥BD AC=BD AC⊥BD且AC=BD
【解析】
首先连接AC,BD,由三角形中位线的性质,可判定EH∥FG,GH∥EF,继而可证得四边形EFGH是平行四边形;
a、由EFGH是平行四边形可得当原四边形ABCD的对角线AC、BD满足AC⊥BD时,四边形EFGH是矩形;
b、由EFGH是平行四边形可得原四边形ABCD的对角线AC、BD满足AC=BD时,四边形EFGH是菱形;
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
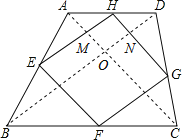
连接AC,BD,
∵四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
∴EH∥BD,FG∥BD,
∴EH∥FG,
同理:GH∥EF,
∴四边形EFGH是平行四边形.
a、当AC⊥BD时,四边形EFGH是矩形.
∵由①得:四边形MONH是平行四边形,
∴当AC⊥BD时,四边形MONH是矩形,
∴∠EHG=90°,
∴四边形EFGH是矩形.
b、当AC=BD时,四边形EFGH是菱形.
∵HG= ![]() AC,EH=
AC,EH= ![]() BD,
BD,
∴EH=GH,
∴四边形EFGH是菱形;
c、由a与b可得:原四边形ABCD的对角线AC、BD满足AC⊥BD且AC=BD时,四边形EFGH是正方形.
故答案为:a、AC⊥BD,b、AC=BD,c、AC⊥BD且AC=BD.
-
科目: 来源: 题型:
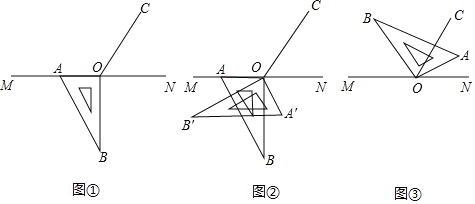
查看答案和解析>>【题目】如图①,点O为直线MN上一点,过点O作直线OC,使∠NOC=60°.将一把直角三角尺的直角顶点放在点O处,一边OA在射线OM上,另一边OB在直线AB的下方,其中∠OBA=30°
(1)将图②中的三角尺沿直线OC翻折至△A′B′O,求∠A′ON的度数;
(2)将图①中的三角尺绕点O按每秒10°的速度沿顺时针方向旋转,旋转角为α(0<α<360°),在旋转的过程中,在第几秒时,直线OA恰好平分锐角∠NOC;
(3)将图①中的三角尺绕点O顺时针旋转,当点A点B均在直线MN上方时(如图③所示),请探究∠MOB与∠AOC之间的数量关系,请直接写出结论,不必写出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当自然数
 的个位数分别为0,1,2,…,9时,
的个位数分别为0,1,2,…,9时, 的个位数如表所示:
的个位数如表所示: 个位数
个位数0
1
2
3
4
5
6
7
8
9
 个位数
个位数0
1
4
9
6
5
6
9
4
1
 个位数
个位数0
1
8
7
4
5
6
3
2
9
 个位数
个位数0
1
6
1
6
5
6
1
6
1
······
在10,11,12,13这四个数中,当
 ____________时,和数
____________时,和数 能被5整除.
能被5整除. -
科目: 来源: 题型:
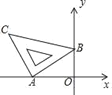
查看答案和解析>>【题目】如图,将含45°角的直角三角尺放置在平面直角坐标系中,其中A(﹣2,0),B(0,1),则直线BC的函数表达式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )
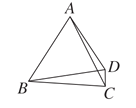
A. 120°B. 135°C. 145°D. 150°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
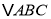 中,
中,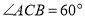 ,
,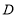 为
为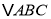 边
边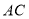 上一点,
上一点,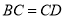 ,
,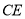 平分
平分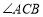 的外角,且
的外角,且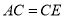 .连接
.连接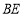 交
交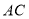 于
于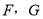 为边
为边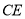 上一点,满足
上一点,满足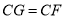 ,连接
,连接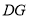 交
交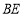 于
于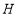 .以下结论:①
.以下结论:①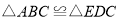 ;②
;②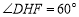 ;③
;③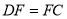 ;④若
;④若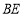 平分
平分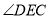 ,则
,则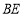 平分
平分 正确的是_____________.
正确的是_____________.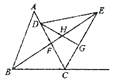
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )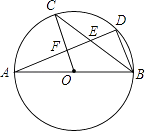
A.②④⑤⑥
B.①③⑤⑥
C.②③④⑥
D.①③④⑤
相关试题

