【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) (1)A(2,0);C(0,4);(2) 直线CD解析式为y=-![]() x+4.(3)P1(0,0);P2(
x+4.(3)P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).
【解析】
试题分析:(1)已知直线y=-2x+4与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,最后即可求出CD的解析式;
(3)将点P在不同象限进行分类,根据全等三角形的判定方法找出所有全等三角形,找出符合题意的点P的坐标.
试题解析:(1)A(2,0);C(0,4)
(2)由折叠知:CD=AD.设AD=x,则CD=x,BD=4-x,
根据题意得:(4-x)2+22=x2解得:x=![]()
此时,AD=![]() ,D(2,
,D(2,![]() )
)
设直线CD为y=kx+4,把D(2,![]() )代入得
)代入得![]() =2k+4
=2k+4
解得:k=-![]()
∴该直线CD解析式为y=-![]() x+4.
x+4.
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图,
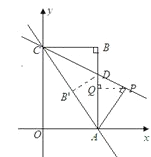
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=![]() ,PD=BD=4-
,PD=BD=4-![]() =
=![]() ,AP=BC=2
,AP=BC=2
由AD×PQ=DP×AP得:![]() PQ=3
PQ=3
∴PQ=![]()
∴xP=2+![]() =
=![]() ,
,
把x=![]() 代入y=-
代入y=-![]() x+4得y=
x+4得y=![]()
此时P(![]() ,
,![]() )
)
(也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标)
③当点P在第二象限时,如图
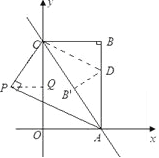
同理可求得:CQ=![]()
∴OQ=4-![]() =
=![]()
此时P(-![]() ,
,![]() )
)
综合得,满足条件的点P有三个,
分别为:P1(0,0);P2(![]() ,
,![]() );P3(-
);P3(-![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )

A.41
B.40
C.39
D.38 -
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车制造厂开发了一款新式自行车,计划6月份生产安装600辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人:他们经过培训后也能独立进行安装.调研部门发现:1名热练工和2名新工人每日可安装8辆自行车;2名熟练工和3名新工人每日可安装14辆自行车.
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘n名新工人(0<n<10).使得招聘的新工人和抽调熟练工刚好能完成6月份(30天) 的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为11千公里;如安装在后轮,安全行使路程为9千公里.请问一对轮胎能行使的最长路程是多少千公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )
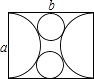
A.b=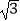 a
a
B.b=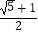 a
a
C.b=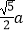
D.b=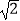 a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 是线段
是线段 上的一点,
上的一点, .动点
.动点 从点
从点 出发,以
出发,以 的速度向右运动,到达点
的速度向右运动,到达点 后立即返回,以
后立即返回,以 的速度向左运动;动点
的速度向左运动;动点 从点
从点 出发,以
出发,以 的速度向右运动. 设它们同时出发,运动时间为
的速度向右运动. 设它们同时出发,运动时间为 . 当点
. 当点 与点
与点 第二次重合时,
第二次重合时, 两点停止运动.
两点停止运动. (1)求
 ,
, ;
;(2)当
 为何值时,
为何值时, ;
;(3)当
 为何值时,
为何值时, 与
与 第一次相遇;
第一次相遇;(4)当
 为何值时,
为何值时, .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
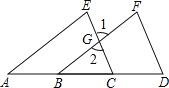
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
-
科目: 来源: 题型:
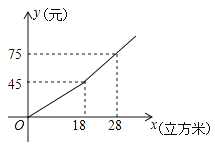
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
相关试题

