【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
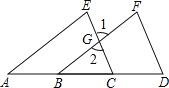
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
参考答案:
【答案】(1)AE;BF;F;F;(2)答案见解析
【解析】
(1)由∠1=∠E,根据内错角相等,两直线平行得到AE∥BF;由CE∥DF,根据两直线平行,内错角相等∠1=∠F,然后利用等量代换得到∠E=∠F;
(2)应用了平行线的判定与性质定理.
(1)因为∠1=∠E(已知),所以AE∥BF;
因为CE∥DF(已知),所以∠1=∠F.
所以∠E=∠F.
(2)(1)的推理中应用了内错角相等,两直线平行和两直线平行,内错角相等.
故答案为:AE,BF,F,F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )
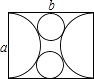
A.b=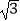 a
a
B.b=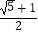 a
a
C.b=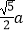
D.b=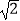 a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 是线段
是线段 上的一点,
上的一点, .动点
.动点 从点
从点 出发,以
出发,以 的速度向右运动,到达点
的速度向右运动,到达点 后立即返回,以
后立即返回,以 的速度向左运动;动点
的速度向左运动;动点 从点
从点 出发,以
出发,以 的速度向右运动. 设它们同时出发,运动时间为
的速度向右运动. 设它们同时出发,运动时间为 . 当点
. 当点 与点
与点 第二次重合时,
第二次重合时, 两点停止运动.
两点停止运动. (1)求
 ,
, ;
;(2)当
 为何值时,
为何值时, ;
;(3)当
 为何值时,
为何值时, 与
与 第一次相遇;
第一次相遇;(4)当
 为何值时,
为何值时, .
.
-
科目: 来源: 题型:
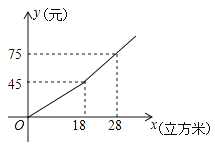
查看答案和解析>>【题目】某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(2m+3)x+m-1.
(1)若函数图象经过原点,求m的值;
(2)若函数图象与y轴上的的交点位于原点上方,求m的取值范围;
(3)若函数图象平行于直线y=x+1,求m的值;
(4)若该函数的值y随自变量x的增大而减小,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数的图象经过点A(-6,4),B(3,0).
(1)求这个函数的解析式;
(2)画出这个函数的图象;
(3)若该直线经过点(9,m),求m的值;
(4)求△AOB的面积.
相关试题

