【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )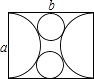
A.b= ![]() a
a
B.b= ![]() a
a
C.b= ![]()
D.b= ![]() a
a
参考答案:
【答案】D
【解析】解:∵半圆的直径为a,
∴半圆的弧长为 ![]()
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,
∴设小圆的半径为r,则:2πr= ![]()
解得:r= ![]()
∴AC= ![]() a﹣r=
a﹣r= ![]() ,
,
如图小圆的圆心为B,半圆的圆心为C,作BA⊥CA于A点,
则:AC2+AB2=BC2
即:( ![]() )2+(
)2+( ![]() )2=(
)2=( ![]() )2
)2
整理得:b= ![]() a
a
故选D.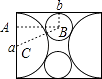
首先利用圆锥形圣诞帽的底面周长等于侧面的弧长求得小圆的半径,然后利用两圆外切的性质求得a、b之间的关系即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a6÷a2=a3
B.(a3)2=a5
C.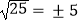
D.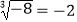
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )

A.41
B.40
C.39
D.38 -
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车制造厂开发了一款新式自行车,计划6月份生产安装600辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人:他们经过培训后也能独立进行安装.调研部门发现:1名热练工和2名新工人每日可安装8辆自行车;2名熟练工和3名新工人每日可安装14辆自行车.
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘n名新工人(0<n<10).使得招聘的新工人和抽调熟练工刚好能完成6月份(30天) 的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为11千公里;如安装在后轮,安全行使路程为9千公里.请问一对轮胎能行使的最长路程是多少千公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,点
,点 是线段
是线段 上的一点,
上的一点, .动点
.动点 从点
从点 出发,以
出发,以 的速度向右运动,到达点
的速度向右运动,到达点 后立即返回,以
后立即返回,以 的速度向左运动;动点
的速度向左运动;动点 从点
从点 出发,以
出发,以 的速度向右运动. 设它们同时出发,运动时间为
的速度向右运动. 设它们同时出发,运动时间为 . 当点
. 当点 与点
与点 第二次重合时,
第二次重合时, 两点停止运动.
两点停止运动. (1)求
 ,
, ;
;(2)当
 为何值时,
为何值时, ;
;(3)当
 为何值时,
为何值时, 与
与 第一次相遇;
第一次相遇;(4)当
 为何值时,
为何值时, .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,点A、B、C、D在一条直线上,填写下列空格:
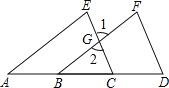
因为∠1=∠E(已知),所以______ // ______ .
因为CE//DF(已知),所以∠1=∠ ______ ,所以∠E=∠ ______ .
(2)说出(1)的推理中应用了哪两个互逆的真命题?
相关试题

