【题目】如图是老年活动中心门口放着的一个招牌,这个招牌是由三个特大号的骰子摞在一起而成的.每个骰子的六个面的点数分别是1到6,其中可以看见7个面,其余11个面是看不见的,则看不见的面上的点数总和是( )
A.41
B.40
C.39
D.38
参考答案:
【答案】C
【解析】解:三个骰子18个面上的数字的总和为:
3(1+2+3+4+5+6)=3×21=63,
看得见的7个面上的数字的和为:
1+2+3+5+4+6+3=24,
所以,看不见的面上的点数总和是63﹣24=39.
故选C.
【考点精析】本题主要考查了常见几何体的三视图的相关知识点,需要掌握俯视图放在主视图的下面,长度与主视图的长度一样;左视图放在主视图的右面,高度与主视图的高度一样,宽度与俯视图的宽度一样,可简记为“长对正;高平齐;宽相等”才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形按一定规律排列,观察并回答:

(1)依照此规律,第四个图形共有 个★,第六个图形共有 个★;
(2)第n个图形中有★ 个;
(3)根据(2)中的结论,第几个图形中有2020个★?
-
科目: 来源: 题型:
查看答案和解析>>【题目】长春市地铁1号线,北起北环站,南至红咀子站,共设15个地下车站,2017年6月30日开通运营,标志着吉林省正式迈进“地铁时代”,15个站点如图所示.

某天,王红从人民广场站开始乘坐地铁,在地铁各站点做志愿者服务,到A站下车时,本次志愿者服务活动结束,约定向红咀子站方向为正,当天的乘车记录如下(单位:站):+5,﹣2,﹣6,+8,+3,﹣4,﹣9,+8
(1)请通过计算说明A站是哪一站?
(2)相邻两站之间的距离为1.3千米,求这次王红志愿服务期间乘坐地铁行进的路程是多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a6÷a2=a3
B.(a3)2=a5
C.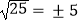
D.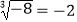
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车制造厂开发了一款新式自行车,计划6月份生产安装600辆,由于抽调不出足够的熟练工来完成新式自行车的安装,工厂决定招聘一些新工人:他们经过培训后也能独立进行安装.调研部门发现:1名热练工和2名新工人每日可安装8辆自行车;2名熟练工和3名新工人每日可安装14辆自行车.
(1)每名熟练工和新工人每日分别可以安装多少辆自行车?
(2)如果工厂招聘n名新工人(0<n<10).使得招聘的新工人和抽调熟练工刚好能完成6月份(30天) 的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)该自行车关于轮胎的使用有以下说明:本轮胎如安装在前轮,安全行使路程为11千公里;如安装在后轮,安全行使路程为9千公里.请问一对轮胎能行使的最长路程是多少千公里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用邻边分别为a,b(a<b)的矩形硬纸板裁出以a为直径的两个半圆,再裁出与矩形的较长边、两个半圆均相切的两个小圆.把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b满足的关系式是( )
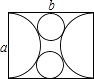
A.b=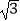 a
a
B.b=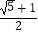 a
a
C.b=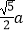
D.b=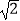 a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
相关试题

