搜索
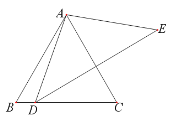
【题目】如图，△ABC是等边三角形，点D在BC上，△ADE是等腰三角形，AD ＝AE ，∠DAE ＝100°，当DE⊥AC时，求∠BAD和∠EDC的度数.
参考答案：
【答案】30°
【解析】
首先利用等边三角形的性质得出∠B=∠BAC=∠C=60°，再利用等腰三角形的性质得出∠ADE＝∠E＝40°，进而得出∠BAD=10°，进而利用三角形外角性质得出答案．
解：∵△ABC是等边三角形
∴∠B=∠BAC=∠C=60°
又∵AD =AE ，∠DAE =100°，
∴∠ADE=∠E =40°
∵DE⊥AC
∴ ∠DAC =∠EAC =50°
∴ ∠BAD=60°-50°=10°
又∵∠ADC=∠B +∠BAD =70°
∴∠EDC =∠ADC -∠ADE =30°
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，E、F、G、H分别在它的四条边上，且
四边形EFGH是什么特殊四边形？你是如何判断的？
-
科目： 来源： 题型：
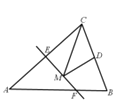
查看答案和解析>>【题目】如图，等腰三角形ABC的底边BC长为6，面积是36，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为______．
-
科目： 来源： 题型：
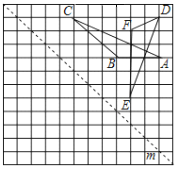
查看答案和解析>>【题目】如图，在由边长均为1个单位长度的小正方形组成的网格中，给出了格点△ABC和△DEF（顶点 为网格线的交点），以及经过格点的直线m．
（1）画出△ABC关于直线m对称的△A1B1C1；
（2）将△DEF先向左平移5个单位长度，再向下平移4个单位长度，画出平移后得到的△D1E1F1；
（3）求∠A+∠E= ________°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC和△DEC都是等腰直角三角形，∠ACB=∠DCE=90°，E在线段AC上，连接AD， BE的延长线交AD于F．
（1）猜想线段BE、AD的数量关系和位置关系：_______________（不必证明）；
（2）当点E为△ABC内部一点时，使点D和点E分别在AC的两侧，其它条件不变．
①请你在图2中补全图形；
②（1）中结论成立吗？若成立，请证明；若不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形
的对角线相交于点
，
，
．
求证：四边形
是菱形；
若
，菱形的面积为
，求
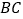的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知A（a，0），B（0，b），且a、b满足
.（1）填空：a= ，b= ；
（2）如图1，将ΔAOB沿x轴翻折得ΔAOC，D为线段AB上一动点，OE⊥OD交AC于点E，求S四边形ODAE。
（3）如图2，D为AB上一点，过点B作BF⊥OD于点G，交x轴于点F，点H为x轴正半轴上一点，∠BFO=∠DHO，求证：AF=OH.
相关试题
